题目内容
若函数y=f(x)为偶函数,且满足f(x+2)=-f(x),当x∈(0,1)时,f(x)=
+1,则f(
)=( )
| x |
| 2 |
| 7 |
| 2 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据已知可得函数y=f(x)是周期为4的周期函数,结合函数为偶函数,可得f(
)=f(-
)=f(
),代入可得答案.
| 7 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
即函数y=f(x)是周期为4的周期函数,
故f(
)=f(-
+4)=f(-
),
又∵函数y=f(x)为偶函数,
∴f(-
)=f(
),
由当x∈(0,1)时,f(x)=
+1得:
f(
)=
,
故f(
)=
,
故选:C
∴f(x+4)=-f(x+2)=f(x),
即函数y=f(x)是周期为4的周期函数,
故f(
| 7 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵函数y=f(x)为偶函数,
∴f(-
| 1 |
| 2 |
| 1 |
| 2 |
由当x∈(0,1)时,f(x)=
| x |
| 2 |
f(
| 1 |
| 2 |
| 5 |
| 4 |
故f(
| 7 |
| 2 |
| 5 |
| 4 |
故选:C
点评:本题考查的知识点是函数的奇偶性,函数的周期性,函数求值,是函数图象和性质的综合应用,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,
=
,
=
,
=
,且满足:|
|=1,|
|=2,|
|=
,则
•
+
•
+
•
的值为( )
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| c |
| 3 |
| a |
| b |
| b |
| c |
| c |
| a |
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
等比数列{an},满足a1=2,公比q=2,则a5=( )
| A、10 | B、16 | C、32 | D、64 |
已知f(x)=x5+2x4+3x3+4x2+5x+6,用秦九韶算法求这个多项式当x=2时的值的过程中,不会出现的结果是( )
| A、11 | B、28 | C、57 | D、120 |
有一段演绎推理:“因为对数函数y=logax是减函数;已知y=log2x是对数函数,所以y=log2x是减函数”,结论显然是错误的,这是因为( )
| A、推理形式错误 |
| B、小前提错误 |
| C、大前提错误 |
| D、非以上错误 |
已知数列{an}满足an+an+1=
(n∈N*),其中a1=-
,试通过计算a2,a3,a4,a5,猜想an等于( )
| (-1)n+1 |
| 2 |
| 1 |
| 2 |
A、an=
| |||||||||
B、an=-
| |||||||||
C、an=
| |||||||||
D、
|
已知动点P(t,t),Q(10-t,0),其中0<t<10,则点M(6,1),N(4,5)与直线PQ的关系是( )
| A、M,N均在直线PQ上 |
| B、M,N均不在直线PQ上 |
| C、M不在直线PQ上,N可能在直线PQ上 |
| D、M可能在直线PQ上,N不在直线PQ上 |
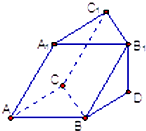 已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )
已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )