题目内容
过椭圆
+
=1的焦点,倾斜角为45°的弦AB的长是 .
| x2 |
| 25 |
| y2 |
| 9 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出椭圆的焦点坐标,根据点斜率式设AB方程,与椭圆方程消去y,利用根与系数的关系,根据弦长公式即可算出弦AB的长.
解答:
解:∵椭圆方程为
+
=1,
∴焦点分别为F1(-4,0),F2(4,0),
∴可设直线AB的方程为y=x+4,
将AB方程与椭圆方程消去y,得34x2+200x+175=0
设A(x1,y1),B(x2,y2),可得
x1+x2=-
,x1x2=
因此,|AB|=
•|x1-x2|=
.
故答案为:
.
| x2 |
| 25 |
| y2 |
| 9 |
∴焦点分别为F1(-4,0),F2(4,0),
∴可设直线AB的方程为y=x+4,
将AB方程与椭圆方程消去y,得34x2+200x+175=0
设A(x1,y1),B(x2,y2),可得
x1+x2=-
| 100 |
| 17 |
| 175 |
| 34 |
因此,|AB|=
| 2 |
| 90 |
| 17 |
故答案为:
| 90 |
| 17 |
点评:本题给出椭圆经过焦点且倾斜角为45°的弦AB,求弦长.着重考查了椭圆的标准方程与简单几何性质、直线与椭圆的位置关系等知识,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目

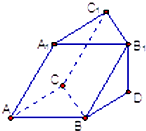 已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )
已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )