题目内容
(1)log2.56.25+lg
+ln
+2 1+log23;
(2)(
×
)6+(
)
-4(
)
-
×80.25+(-2014)0.
| 1 |
| 100 |
| e |
(2)(
| 3 | 2 |
| 3 |
2
|
| 4 |
| 3 |
| 16 |
| 49 |
| 1 |
| 2 |
| 4 | 2 |
考点:对数的运算性质,有理数指数幂的化简求值
专题:函数的性质及应用
分析:(1)利用对数的运算法则即可得出;
(2)利用指数幂的运算法则即可得出.
(2)利用指数幂的运算法则即可得出.
解答:
解:(1)原式=log2.52.52+lg10-2+lne
+2×2log23
=2-2+
+2×3
=
.
(2)原式=(2
×3
)6+(2
)
-4×(
)2×(-
)-2
×2
+1
=22×33+2-4×
-2+1
=108-7+1
=102.
| 1 |
| 2 |
=2-2+
| 1 |
| 2 |
=
| 13 |
| 2 |
(2)原式=(2
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 7 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
=22×33+2-4×
| 7 |
| 4 |
=108-7+1
=102.
点评:本题考查了对数与指数幂的运算法则,属于基础题.

练习册系列答案
相关题目
已知△ABC满足c=2acosB,则△ABC的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
若关于x的不等式cosθ(1-x)2-2x(1-x)+2
x2sinθ≥0对一切x∈[0,1]恒成立,则θ的取值范围是( )
| 2 |
A、[kπ+
| ||||
B、[2kπ+
| ||||
C、[kπ+
| ||||
D、[2kπ+
|
已知空间四边形ABCD,E,F,G,H分别边AB,BC,CD,DA的中点,则EG与FH位置关系是( )
| A、相交 | B、平行 | C、异面 | D、重合 |
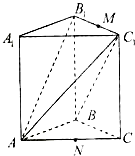 如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点.
如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点.