题目内容
已知f(x+1)=2x+3,则f(x)= .
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由题意得f(x+1)=2(x+1)+1,替换即可.
解答:
解:∵f(x+1)=2(x+1)+1,
∴f(x)=2x+1,
故答案为:2x+1.
∴f(x)=2x+1,
故答案为:2x+1.
点评:本题考查了函数的解析式问题,本题属于基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
若关于x的不等式cosθ(1-x)2-2x(1-x)+2
x2sinθ≥0对一切x∈[0,1]恒成立,则θ的取值范围是( )
| 2 |
A、[kπ+
| ||||
B、[2kπ+
| ||||
C、[kπ+
| ||||
D、[2kπ+
|
已知空间四边形ABCD,E,F,G,H分别边AB,BC,CD,DA的中点,则EG与FH位置关系是( )
| A、相交 | B、平行 | C、异面 | D、重合 |
如图,PA垂直于正方形ABCD所在平面,则以下关系错误的是( )
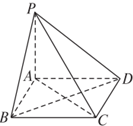

| A、平面PCD⊥平面PAD |
| B、平面PCD⊥平面PBC |
| C、平面PAB⊥平面PBC |
| D、平面PAB⊥平面PAD |
双曲线
-
=1的离心率e∈(1,2),则实数k的取值范围是( )
| x2 |
| 4 |
| y2 |
| k |
| A、(0,4) | ||
| B、(1,1) | ||
C、(0,2
| ||
| D、(0,12) |
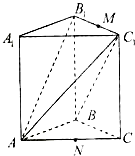 如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点.
如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点. 已知函数f(x)=
已知函数f(x)=