题目内容
两定点的距离为6,点M到这两定点的距离的平方和为26,求M的轨迹方程.
考点:轨迹方程
专题:综合题,直线与圆
分析:以AB所在直线为x轴,AB的垂直平分线为y轴建立平面直角坐标系,设出动点M的坐标,由M到这两定点的距离的平方和为26列等式,整理后得答案.
解答:
解:设两定点分别为A,B,以AB所在直线为x轴,AB的垂直平分线为y轴建立直角坐标系如图:

∵|AB|=6,则A(-3,0),B(3,0),
设M(x,y),
则|MA|2+|MB|2=26,
即(
)2+(
)2=26.
整理得:x2+y2=4.
∴M的轨迹方程是x2+y2=4.

∵|AB|=6,则A(-3,0),B(3,0),
设M(x,y),
则|MA|2+|MB|2=26,
即(
| (x+3)2+y2 |
| (x-3)2+y2 |
整理得:x2+y2=4.
∴M的轨迹方程是x2+y2=4.
点评:本题考查了轨迹方程的求法,解答的关键是建立恰当的平面直角坐标系,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
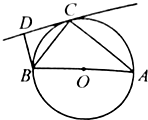 如图,⊙O的直径AB=4,C为圆周上一点,AC=3,CD是⊙O的切线,BD⊥CD于D,则CD=
如图,⊙O的直径AB=4,C为圆周上一点,AC=3,CD是⊙O的切线,BD⊥CD于D,则CD=