题目内容
若x,y∈R且x2+y2=1,则x-y的取值范围为 .
考点:圆的标准方程
专题:直线与圆
分析:设直线t=x-y,利用直线和圆相切的性质即可得到结论.
解答:
解:设t=x-y,
则对应的直线方程为x-y-t=0,
当直线和圆相切时,
满足圆心(0,0)与直线x-y-t=0的距离d=
=1,
即|t|=
,
即t=±
,
∴x-y的取值范围为[-
,
],
故答案为:[-
,
].
则对应的直线方程为x-y-t=0,
当直线和圆相切时,
满足圆心(0,0)与直线x-y-t=0的距离d=
| |t| | ||
|
即|t|=
| 2 |
即t=±
| 2 |
∴x-y的取值范围为[-
| 2 |
| 2 |
故答案为:[-
| 2 |
| 2 |
点评:本题主要考查直线和圆的位置关系的判断,利用直线和圆相切是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
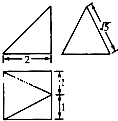
一个几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||||
B、
| ||||
C、4
| ||||
D、
|