题目内容
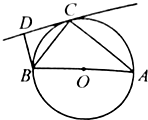如图，⊙O的直径AB=4，C为圆周上一点，AC=3，CD是⊙O的切线，BD⊥CD于D，则CD=考点：与圆有关的比例线段
专题：直线与圆
分析：由已知条件，利用圆的性质和弦切角定理推导出△ACB∽△CDB，由此能求出CD的长．
解答：
解：如图，∵，⊙O的直径AB=4，C为圆周上一点，AC=3，
CD是⊙O的切线，BD⊥CD于D，
∴∠ACB=∠CDB=90°，∠DCB=∠CAB，
∴△ACB∽△CDB，
∴
=
，
∴CD=
=
=
．
故答案为：
．
CD是⊙O的切线，BD⊥CD于D，
∴∠ACB=∠CDB=90°，∠DCB=∠CAB，
∴△ACB∽△CDB，
∴
| AB |
| BC |
| AC |
| CD |
∴CD=
| AC•BC |
| AB |
3×
| ||
| 4 |
3
| ||
| 4 |
故答案为：
3
| ||
| 4 |
点评：本题考查与圆有关的线段长的求法，是中档题，解题时要熟练掌握圆的性质，要注意弦切角定理的合理运用．
练习册系列答案
相关题目
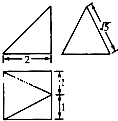
一个几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||||
B、
| ||||
C、4
| ||||
D、
|
已知
=
，
=
，
=
且满足λ（
+
）•
=0（λ＞0），则△ABC为（ ）
| BA |
| a |
| BC |
| b |
| AC |
| c |
| ||
|
|
| ||
|
|
| c |
| A、等腰三角形 | B、等边三角形 |
| C、直角三角形 | D、不确定 |