题目内容
 y=sinx+2|sinx|.
y=sinx+2|sinx|.(1)画出这个函数的图象;
(2)这个函数是周期函数吗?若是,求出它的最小正周期;
(3)指出这个函数的单调增区间.
考点:正弦函数的图象,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)根据零点分段法,将函数解析式化为分段函数,进而可画出函数的图象
(2)根据(1)中函数图象,结合正弦型函数的周期性,可判断函数为周期函数,并能求出最小正周期;
(3)根据函数的图象,分析函数图象上升的范围,可求出函数的单调增区间.
(2)根据(1)中函数图象,结合正弦型函数的周期性,可判断函数为周期函数,并能求出最小正周期;
(3)根据函数的图象,分析函数图象上升的范围,可求出函数的单调增区间.
解答:
解:(1)y=sinx+2|sinx|=
,(k∈Z),
其函数图象如下图所示:
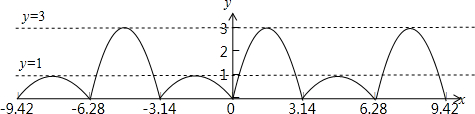
(2)由(1)中函数图象可得:
这上函数是周期函数,
最小正周期为:2π;
(3)由(1)中函数图象可得:
单调增区间为:[2kπ,
+2kπ]和[π+2kπ,
π+2kπ]k∈Z.
|
其函数图象如下图所示:
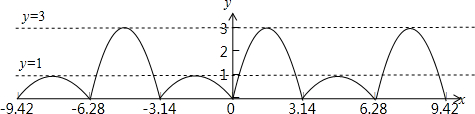
(2)由(1)中函数图象可得:
这上函数是周期函数,
最小正周期为:2π;
(3)由(1)中函数图象可得:
单调增区间为:[2kπ,
| π |
| 2 |
| 3 |
| 2 |
点评:本题考查的知识点是正弦函数的图象,三角函数的周期性及其求法,函数的单调区间,其中画出函数图象是解答的关键.

练习册系列答案
相关题目
 已知函数f(x)=-x3+ax2+bx在区间(-2,1)内,当x=-1时取得极小值,当
已知函数f(x)=-x3+ax2+bx在区间(-2,1)内,当x=-1时取得极小值,当