题目内容
如果a>b,给出下列不等式:(1)
<
;(2)a3>b3;(3)a2+1>b2+1;(4)2a>2b.其中正确的是 .(把你认为正确的序号填上)
| 1 |
| a |
| 1 |
| b |
考点:不等关系与不等式,不等式比较大小
专题:函数的性质及应用
分析:(1)取a=2,b=-1,满足a>b,但是
<
;不成立;
(2)利用函数f(x)=x3在R上单调递增即可得出;
(3)取a=1,b=-2,满足a>b,但是a2+1>b2+1不成立;
(4)利用指数函数f(x)=2x在R上单调递增即可得出.
| 1 |
| a |
| 1 |
| b |
(2)利用函数f(x)=x3在R上单调递增即可得出;
(3)取a=1,b=-2,满足a>b,但是a2+1>b2+1不成立;
(4)利用指数函数f(x)=2x在R上单调递增即可得出.
解答:
解:(1)取a=2,b=-1,满足a>b,但是
<
;不成立;
(2)利用函数f(x)=x3在R上单调递增可得:a3>b3;
(3)取a=1,b=-2,满足a>b,但是a2+1>b2+1不成立;
(4)利用指数函数f(x)=2x在R上单调递增可得:2a>2b.
其中成立的不等式有(2)(4).
故答案为:(2)(4).
| 1 |
| a |
| 1 |
| b |
(2)利用函数f(x)=x3在R上单调递增可得:a3>b3;
(3)取a=1,b=-2,满足a>b,但是a2+1>b2+1不成立;
(4)利用指数函数f(x)=2x在R上单调递增可得:2a>2b.
其中成立的不等式有(2)(4).
故答案为:(2)(4).
点评:本题考查了指数函数、幂函数的单调性、不等式的性质,属于基础题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
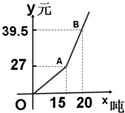 自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示. y=sinx+2|sinx|.
y=sinx+2|sinx|.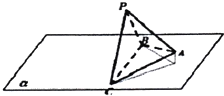 我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高为h,BC在平面α上,现让它绕BC转动,并使它在某一时刻在平面α上的射影是等腰直角三角形,则h的取值范围是
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高为h,BC在平面α上,现让它绕BC转动,并使它在某一时刻在平面α上的射影是等腰直角三角形,则h的取值范围是