题目内容
直线x-2y+m=0与曲线y=
相切,则切点的坐标为 .
| x |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:设直线与曲线相切于点P(x0,y0),根据导数的几何意义可得,
•
=
,解得x0的值,可得切点坐标.
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| 2 |
解答:
解:设直线与曲线相切于点P(x0,y0),则y=
的导数y′=
.
由题意知直线的斜率k=
,即
•
=
,解得x0=1.
因此,切点的坐标为(1,1).
故答案为:(1,1)
| x |
| 1 |
| 2 |
| 1 | ||
|
由题意知直线的斜率k=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| 2 |
因此,切点的坐标为(1,1).
故答案为:(1,1)
点评:本题主要考查导数的几何意义,曲线在该点的切线的斜率,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
抛掷三枚质地均匀硬币,至少一次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 y=sinx+2|sinx|.
y=sinx+2|sinx|.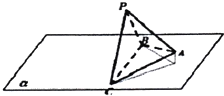 我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高为h,BC在平面α上,现让它绕BC转动,并使它在某一时刻在平面α上的射影是等腰直角三角形,则h的取值范围是
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高为h,BC在平面α上,现让它绕BC转动,并使它在某一时刻在平面α上的射影是等腰直角三角形,则h的取值范围是