一个几何体的三视图如图所示.则这个几何体的体积是( )A．$2\sqrt{3}$B．$\frac{{2\sqrt{3}}}{3}$C．$\frac{4}{3}$D．$\frac{8}{3}$ 题目和参考答案——青夏教育精英家教网——

题目内容

17．一个几何体的三视图如图所示，则这个几何体的体积是（　　）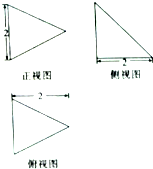

A．

$2\sqrt{3}$

B．

$\frac{{2\sqrt{3}}}{3}$

C．

$\frac{4}{3}$

D．

$\frac{8}{3}$

分析由题设及图知，此几何体为一个三棱锥，其侧面为一个腰长为2的等腰直角三角形，即可求出棱锥的体积．

解答解：由题设及图知，此几何体为一个三棱锥，其侧面为一个腰长为2的等腰直角三角形，
此棱锥的体积为$\frac{1}{3}×2×2=\frac{4}{3}$，
故选：C．

点评本题考查了利用空间几何体的三视图求体积的应用问题，是基础题目．

练习册系列答案

本土教辅赢在暑假高效假期总复习云南科技出版社系列答案

暑假作业北京艺术与科学电子出版社系列答案

黄冈状元成才路暑假作业新疆人民出版社系列答案

暑假特训浙江大学出版社系列答案

名师一号假期作业暑假作业河北教育出版社系列答案

第三学期赢在暑假系列答案

暑假作业宁夏人民教育出版社系列答案

优化学习暑假40天江苏人民出版社系列答案

快乐暑假学段衔接提升方案新疆美术摄影出版社系列答案

假期作业济南出版社系列答案

相关题目

10．已知2^a=3^b=6^c，若$\frac{a+b}{c}$∈（k，k+1），则整数k的值是4．

8．给定两个命题，命题p：对?x∈R，不等式ax²+ax+1＞0恒成立，命题q：关于x方程x²-x+a=0有实数根；若p∧q为假命题，p∨q为真命题，求实数a范围．

5．已知数列{a_n}中，a₁=4，a_n+1=2（a_n+2ⁿ），若不等式2n²-n-3＜λa_n对?n∈N^*恒成立，则实数λ的取值范围是$（\frac{3}{8}，+∞）$．

12．已知函数f（x）=tan（x-$\frac{π}{3}$），一条与x轴平行的直线与函数f（x）的图象相交，则相邻的两个交点之间的距离为π．

2．设是a，b两条不同的直线，α，β是两个不同的平面，且a?α，b?β，（　　）

若α⊥β，则a⊥β

若α⊥β，则a⊥b

若α∥β，则a∥b

若α∥β，则a∥β

9．已知点A（0，-1），抛物线C：y²=2px（p＞0）的焦点为F，直线AF与抛物线C在第一象限交于M点，$\overrightarrow{AF}=\overrightarrow{FM}$，O为坐标原点，则△OAM的面积为（　　）

$\frac{{\sqrt{2}}}{2}$

$\frac{{\sqrt{2}}}{4}$

6．直线y=x+b平分圆x²+y²-8x+2y-2=0的周长，则b=（　　）

7．已知函数f（x）=ax³+bx²+cx在x=±1处取得极值，且在x=0处的切线的斜率为-3，求f（x）的解析式．