题目内容
5.已知数列{an}中,a1=4,an+1=2(an+2n),若不等式2n2-n-3<λan对?n∈N*恒成立,则实数λ的取值范围是$(\frac{3}{8},+∞)$.分析 an+1=2(an+2n),变形为$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=1,利用等差数列的通项公式可得:an=(n+3)•2n.不等式2n2-n-3<λan对?n∈N*恒成立,化为λ>$\frac{2n-3}{{2}^{n}}$=bn,再利用数列{bn}的单调性即可得出.
解答 解:∵an+1=2(an+2n),∴$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=1,
∴数列$\{\frac{{a}_{n}}{{2}^{n}}\}$是等差数列,公差为1,首项为2.
∴$\frac{{a}_{n}}{{2}^{n}}$=2+(n-1)=n+1.
∴an=(n+3)•2n.
不等式2n2-n-3<λan对?n∈N*恒成立,
∴λ>$\frac{2{n}^{2}-n-3}{(n+3)•{2}^{n}}$=$\frac{2n-3}{{2}^{n}}$=bn,
b1<0,n≥2时,bn>0,
bn+1-bn=$\frac{2n-1}{{2}^{n+1}}$-$\frac{2n-3}{{2}^{n}}$=$\frac{5-2n}{{2}^{n+1}}$,
可得n=2时,b2<b3,
n≥3时,数列{bn}单调递减.
因此n=3时,bn取得最大值,b3=$\frac{3}{8}$.
∴$λ>\frac{3}{8}$.
故答案为:$(\frac{3}{8},+∞)$.
点评 本题考查了数列递推关系、等差数列的通项公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知数列{an}中,a1=$\frac{4}{5}$,an+1=$\left\{\begin{array}{l}2{a_n}\;\;\;\;\;\;(0≤{a_n}≤1)\\ 2{a_n}-2\;(1<{a_n}≤2)\end{array}$,则a2015等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
10.在复平面内,复数6-5i,-2+3i对应的点分别为A、B,若C为线段AB的中点,则点C对应的复数是( )
| A. | 4+8i | B. | 8+2i | C. | 2-i | D. | 4+i |
17.一个几何体的三视图如图所示,则这个几何体的体积是( )
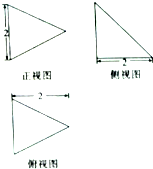

| A. | $2\sqrt{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
15.函数f(x)=ex-x-1的最小值是( )
| A. | -ln2 | B. | $-\sqrt{2}$ | C. | 0 | D. | 1 |
 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,M是PD的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,M是PD的中点. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.