题目内容
12.已知函数f(x)=tan(x-$\frac{π}{3}$),一条与x轴平行的直线与函数f(x)的图象相交,则相邻的两个交点之间的距离为π.分析 利用正切函数的图象与正切函数的周期求解即可.
解答 解:函数f(x)=tan(x-$\frac{π}{3}$),一条与x轴平行的直线与函数f(x)的图象相交,可得函数的图象的相邻两个交点的距离是函数f(x)=tan(x-$\frac{π}{3}$)的周期,可得T=π.
故答案为:π.
点评 本题考查正切函数的周期的应用,正切函数的图象的性质,考查计算能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
20.已知数列{an}中,a1=$\frac{4}{5}$,an+1=$\left\{\begin{array}{l}2{a_n}\;\;\;\;\;\;(0≤{a_n}≤1)\\ 2{a_n}-2\;(1<{a_n}≤2)\end{array}$,则a2015等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
17.一个几何体的三视图如图所示,则这个几何体的体积是( )
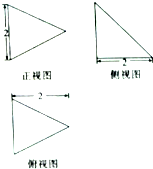

| A. | $2\sqrt{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
2.圆的极坐标方程为ρ=2(cosθ+sinθ),则该圆的圆心极坐标是( )
| A. | $({1,\frac{π}{4}})$ | B. | ($\sqrt{2}$,$\frac{π}{4}$) | C. | ($\frac{1}{2}$,$\frac{π}{4}$) | D. | $({2,\frac{π}{4}})$ |
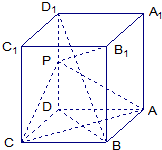 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求:
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求: