题目内容
10.已知2a=3b=6c,若$\frac{a+b}{c}$∈(k,k+1),则整数k的值是4.分析 把指数式化为对数式,再利用对数的运算性质即可得出.
解答 解:设2a=3b=6c=m>0,m≠1.
则a=log2m,b=log3m,c=log6m
则$\frac{a+b}{c}$=$\frac{\frac{lgm}{lg2}+\frac{lgm}{lg3}}{\frac{lgm}{lg6}}$=$\frac{l{g}^{2}6}{lg2lg3}$>$\frac{l{g}^{2}6}{(\frac{lg2+lg3}{2})^{2}}$=4,
∵$\frac{a+b}{c}$∈(k,k+1),∈(k,k+1),则整数k=4.
故答案为:4.
点评 本题考查了指数式化为对数式、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
1.已知集合M={0,1,2,3},N={x|y=$\sqrt{2-x}$},则M∩N=( )
| A. | {0,1} | B. | {1,2} | C. | {0,1,2} | D. | {2,3,4} |
15.若f(x)=$\sqrt{x+1}$,则f(2)=( )
| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
2.下列函数是偶函数的是( )
| A. | y=x3 | B. | y=3x | C. | y=2x2-1 | D. | y=x2+2x-1 |
17.一个几何体的三视图如图所示,则这个几何体的体积是( )
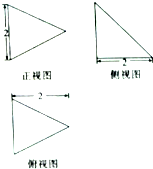

| A. | $2\sqrt{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,M是PD的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,M是PD的中点.