题目内容
9.已知点A(0,-1),抛物线C:y2=2px(p>0)的焦点为F,直线AF与抛物线C在第一象限交于M点,$\overrightarrow{AF}=\overrightarrow{FM}$,O为坐标原点,则△OAM的面积为( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
分析 利用已知条件求出F,通过中点坐标公式求出M,代入抛物线方程,求出p,然后求解三角形的面积.
解答 解:抛物线C:y2=2px(p>0)的焦点为F($\frac{p}{2}$,0),点A(0,-1),直线AF与抛物线C在第一象限交于M点,$\overrightarrow{AF}=\overrightarrow{FM}$,可得M(p,1),
则1=2p2,解得p=$\frac{\sqrt{2}}{2}$.
S△OAM=2S△OAF=2×$\frac{1}{2}$×$1×\frac{\sqrt{2}}{4}$=$\frac{\sqrt{2}}{4}$.
故选:D.
点评 本题考查直线与抛物线的位置关系的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
2.下列函数是偶函数的是( )
| A. | y=x3 | B. | y=3x | C. | y=2x2-1 | D. | y=x2+2x-1 |
20.已知数列{an}中,a1=$\frac{4}{5}$,an+1=$\left\{\begin{array}{l}2{a_n}\;\;\;\;\;\;(0≤{a_n}≤1)\\ 2{a_n}-2\;(1<{a_n}≤2)\end{array}$,则a2015等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
17.一个几何体的三视图如图所示,则这个几何体的体积是( )
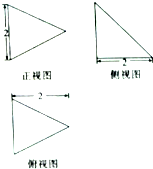

| A. | $2\sqrt{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
19.椭圆$\frac{x^2}{9}$+$\frac{y^2}{4}$=1上一点M到直线x+2y-10=0的距离的最小值为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 1 |