题目内容
7.已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,求f(x)的解析式.分析 由函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,求导,可得±1是f′(x)=0的两根,且f′(0)=-3,解方程组即可求得,a,b,c的值,从而求得f(x)的解析式
解答 解:f'(x)=3ax2+2bx+c,
依题意$\left\{\begin{array}{l}{f′(1)=3a+2b+c=0}\\{f′(-1)=3a-2b+c}\\{f′(0)=c=-3}\end{array}\right.$
解得a=1,b=0,c=-3,
∴f(x)=x3-3x
点评 本题考查利用导数研究函数的单调性和极值问题,考查利用导数研究曲线上某点的切线问题,属于基础题.

练习册系列答案
相关题目
17.一个几何体的三视图如图所示,则这个几何体的体积是( )
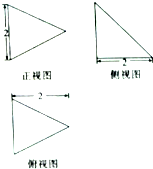

| A. | $2\sqrt{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
15.函数f(x)=ex-x-1的最小值是( )
| A. | -ln2 | B. | $-\sqrt{2}$ | C. | 0 | D. | 1 |
2.圆的极坐标方程为ρ=2(cosθ+sinθ),则该圆的圆心极坐标是( )
| A. | $({1,\frac{π}{4}})$ | B. | ($\sqrt{2}$,$\frac{π}{4}$) | C. | ($\frac{1}{2}$,$\frac{π}{4}$) | D. | $({2,\frac{π}{4}})$ |
19.椭圆$\frac{x^2}{9}$+$\frac{y^2}{4}$=1上一点M到直线x+2y-10=0的距离的最小值为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 1 |