题目内容

6．直线y=x+b平分圆x2+y2-8x+2y-2=0的周长，则b=（　　）
A．3B．5C．-3D．-5

分析 由直线y=x+b平分圆x2+y2-8x+2y-2=0的周长，可知圆的圆心在直线上，用点的坐标适合直线的方程求解．

解答 解：∵直线y=x+b平分圆x2+y2-8x+2y-2=0的周长
∴圆的圆心在直线上
即（4，-1）适合直线y=x+b
∴b=-5
故选D．

点评 本题通过直线与圆的位置关系来考查点与线的位置关系．

练习册系列答案
相关题目
19．已知公差为d的等差数列{an}和公比q＜0的等比数列{bn}，a1=b1=1，a2+b2=1，a3+b3=4
（1）求数列{an}和{bn}的通项公式；
（2）令cn=2${\;}^{{a}_{n}}$•bn2（n∈N*），抽去数列{cn}的第1项、第4项、第7项、…、第（3n-2）项、…，余下的项的顺序不变，构成一个新的数列{dn}求数列{dn}的前n项和Sn．
17．一个几何体的三视图如图所示，则这个几何体的体积是（　　）
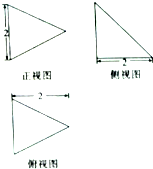
A．$2\sqrt{3}$B．$\frac{{2\sqrt{3}}}{3}$C．$\frac{4}{3}$D．$\frac{8}{3}$
14．如图，AB=AC=BD=1，AB?平面α，AC⊥平面α，BD⊥AB，BD与平面α成30°角，则C、D间的距离为$\sqrt{2}$
1．若函数f（x）同时满足：
①对于定义域上的任意x，恒有f（x）+f（-x）=0
②对于定义域上的任意x1，x2，当x1≠x2时，恒有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}＜0$，则称函数f（x）为“理想函数”．
给出下列四个函数中：
①$f（x）=\frac{1}{x}$；
②f（x）=x2； 
③f（x）=-x；
④$f（x）=\left\{{\begin{array}{l}{-{x^2}}&{x≥0}\\{{x^2}}&{x＜0}\end{array}}\right.$
能被称为“理想函数”的有（　　）个．
A．1B．2C．3D．4
11．△ABC中，sinA=cosB=$\frac{4}{5}$，BC=5，则△ABC的面积为（　　）
A．$\frac{21}{8}$B．6C．$\frac{21}{8}$或6D．$\frac{21}{8}$或$\frac{75}{8}$
18．已知向量$\overrightarrow a$=（1，0），$\overrightarrow b$=（-$\frac{1}{2}$，$\frac{{\sqrt{3}}}{2}$），则$\overrightarrow a$与$\overrightarrow b$的夹角为120°．
15．函数f（x）=ex-x-1的最小值是（　　）
A．-ln2B．$-\sqrt{2}$C．0D．1
16．设函数f（x）=$\overrightarrow m$•$\overrightarrow n$，其中向量$\overrightarrow m$=（2cosx，1），$\overrightarrow n$=（cosx，$\sqrt{3}$sin2x），x∈R．
（1）求f（x）的最小正周期与单调递减区间；
（2）在△ABC中，a、b、c分别是角A、B、C的对边，已知f（A）=2，b=1，△ABC的面积为$\frac{{\sqrt{3}}}{2}$，求a．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网