题目内容
15.已知集合A={x|(x+1)(x-2)<0},非空集合B={x|2a<x<6},则“A∩B=∅”的充分不必要条件可以是( )| A. | -1<a<2 | B. | 1≤a<3 | C. | a>0 | D. | 1<a<3 |
分析 若A∩B=∅,则2≤2a<6,解得:1≤a<3,则“A∩B=∅”的充分不必要条件为[1,3)的真子集,进而得到答案.
解答 解:∵集合A={x|(x+1)(x-2)<0}=(-1,2),
非空集合B={x|2a<x<6},
若A∩B=∅,则2≤2a<6,
解得:1≤a<3,
则“A∩B=∅”的充分不必要条件为[1,3)的真子集,
比照四个答案,可得D答案符号要求,
故选:D.
点评 本题考查的知识点是充要条件的定义,集合的包含关系及应用,难度中档.

练习册系列答案
相关题目
17.三次函数$f(x)=a{x^3}-\frac{3}{2}{x^2}+2x+1$的图象在点(1,f(1))处的切线与x轴平行,则f(x)在区间(1,3)上的最小值是( )
| A. | $\frac{8}{3}$ | B. | $\frac{11}{6}$ | C. | $\frac{11}{3}$ | D. | $\frac{5}{3}$ |
4.已知sinα+cosα=$\frac{\sqrt{3}}{2}$,且α∈(0,π),则sin2α的值为( )
| A. | -$\frac{\sqrt{15}}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{\sqrt{15}}{4}$ | D. | $\frac{1}{4}$ |
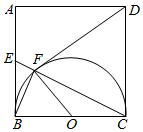 如图,正方形ABCD中,E是AB的中点,CE与以BC为直径的半圆O交于点F,C
如图,正方形ABCD中,E是AB的中点,CE与以BC为直径的半圆O交于点F,C