题目内容
10.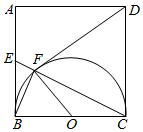 如图,正方形ABCD中,E是AB的中点,CE与以BC为直径的半圆O交于点F,C
如图,正方形ABCD中,E是AB的中点,CE与以BC为直径的半圆O交于点F,C(Ⅰ)证明:DF与圆O相切
(Ⅱ)证明:△DCF∽△OBF.
分析 (Ⅰ)连接OD,通过证明:△FOD≌△COD,得到∠DFO=∠DCO=90°,即可证明DF与圆O相切;
(Ⅱ)通过证明:$\frac{DF}{OF}=\frac{DC}{OB}$,即可证明△DCF∽△OBF.
解答  (Ⅰ)证明:连接OD,
(Ⅰ)证明:连接OD,
∵正方形ABCD中,E、O分别是AB、BC的中点,
∴EB=OC,
∵BC=CD,∠EBC=∠OCD=90°,
∴△EBC≌△OCD,
∴∠BEC=∠COD,
∵BF⊥EC,
∴∠BEC=∠FBC,
∴∠FBC=∠COD,
∴BF∥OD,
∴∠BFO=∠FOD,
∴∠FPD=∠COD,
∵OF=OC,OD=OD,∴△FOD≌△COD,
∴∠DFO=∠DCO=90°,
∴DF与圆O相切;
(Ⅱ)由(Ⅰ)得∠DFO=∠DCO=90°,
∴∠DFO+∠DCO=180°,
∴C,D,F,O四点共圆,
∴∠BOF=∠CDF,
∵DF=DC,
∴$\frac{DF}{OF}=\frac{DC}{OB}$,
∴△DCF∽△OBF.
点评 本题考查直线与圆的位置关系,考查三角形全等的证明,考查三角形相似的证明,属于中档题.

练习册系列答案
相关题目
12.一个几何体的三视图如图所示,则此几何体的表面积为( )
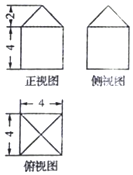

| A. | $80+16\sqrt{2}$ | B. | $96+13\sqrt{2}$ | C. | 96 | D. | 112 |
15.已知集合A={x|(x+1)(x-2)<0},非空集合B={x|2a<x<6},则“A∩B=∅”的充分不必要条件可以是( )
| A. | -1<a<2 | B. | 1≤a<3 | C. | a>0 | D. | 1<a<3 |
2.已知随机变量ε的分布列如下表:
求其数学期望、方差和标准差.
| ε | 0 | 1 | 2 | 3 | 4 |
| p | 0.2 | 0.4 | 0.3 | 0.08 | 0.02 |
 已知函数f(x)=sin(2x+$\frac{π}{4}$)+1.
已知函数f(x)=sin(2x+$\frac{π}{4}$)+1.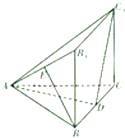 如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.
如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.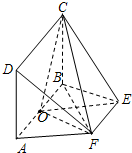 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.