题目内容
10.已知在直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,AB=AC=4,AA1=a.棱BB1的中点为E,棱B1C1的中点为F,平面AEF与平面AA1C1C的交线与AA1所成角的正切值为$\frac{2}{3}$,则三棱柱ABC-A1B1C1外接球的半径为$2\sqrt{3}$.分析 由题意画出图形,求解直角三角形求出a,然后补形可得三棱柱ABC-A1B1C1外接球的半径.
解答 解:如图,连接EF并延长交CC1 的延长线于G,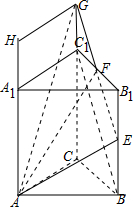
连接AG,在平面ACC1 内过G作GH交AA1 的延长线于H,
则AH=$\frac{3}{2}a$,GH=AC=4,
∴$tan∠GAH=\frac{GH}{AH}=\frac{4}{\frac{3}{2}a}=\frac{2}{3}$,得a=4.
把原直三棱柱补形为正方体,则正方体的棱长为4.
∴三棱柱ABC-A1B1C1外接球的半径r=$\frac{1}{2}\sqrt{{4}^{2}+{4}^{2}+{4}^{2}}=2\sqrt{3}$.
故答案为:$2\sqrt{3}$.
点评 本题考查球的体积与表面积,考查空间想象能力和思维能力,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
5.已知关于x的方程e2x+ex-a=0有实数解,则实数a的取值范围是( )
| A. | [0,+∞) | B. | (0,+∞) | C. | (1,2) | D. | (1,+∞) |
15.三棱锥A-BCD中,△ABC为等边三角形,AB=2$\sqrt{3}$,∠BDC=90°,二面角A-BC-D的大小为150°,则三棱锥A-BCD的外接球的表面积为( )
| A. | 7π | B. | 12π | C. | 16π | D. | 28π |