题目内容
19.已知实数x,y满足$\left\{\begin{array}{l}{x-3≤0}\\{y-1≥0}\\{x-y+1≥0}\end{array}\right.$,若ax+y的最大值为10,则实数a=( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 画出满足条件的平面区域,判断最优解的位置,将点的坐标代入求出a的值即可.
解答  解:画出满足条件的平面区域,如图示:
解:画出满足条件的平面区域,如图示:
由$\left\{\begin{array}{l}{x=3}\\{x-y+1=0}\end{array}\right.$,解得A(3,4),
令z=ax+y,因为z的最大值为10,
所以直线在y轴上的截距的最大值为10,即直线过(0,10),
所以z=ax+y与可行域有交点,
当a>0时,
直线经过A时z取得最大值.
即ax+y=10,将A(3,4)代入得:
3a+4=10,解得:a=2,
当a≤0时,
直线经过A时z取得最大值.
即ax+y=10,将A(3,4)代入得:
3a+4=10,解得:a=2,与a≤0矛盾,
综上:a=2.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.对任意x∈[0,$\frac{π}{6}$],任意y∈(0,+∞),不等式$\frac{y}{4}$-2cos2x≥asinx-$\frac{9}{y}$恒成立,则实数a的取值范围是( )
| A. | (-∞,3] | B. | [-2$\sqrt{2}$,3] | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-3,3] |
7.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
4.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\frac{1}{2}$,则$\overrightarrow{a}$+2$\overrightarrow{b}$与$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
9.椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右焦点分别为F1、F2,过F2作x轴的垂线交椭圆于点P,过P与原点O的直线交椭圆于另一点Q,则△F1PQ的周长为( )
| A. | 4 | B. | 8 | C. | $4+\sqrt{13}$ | D. | $2+\sqrt{13}$ |
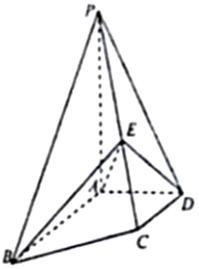 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.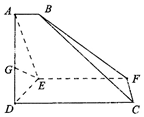 如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.