题目内容
15.三棱锥A-BCD中,△ABC为等边三角形,AB=2$\sqrt{3}$,∠BDC=90°,二面角A-BC-D的大小为150°,则三棱锥A-BCD的外接球的表面积为( )| A. | 7π | B. | 12π | C. | 16π | D. | 28π |
分析 由题意画出图形,通过求解直角三角形可得三棱锥A-BCD的外接球的半径,代入球的表面积公式得答案.
解答 解:设球心为M,BC的中点为P,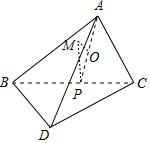
∵三角形BDC满足∠BDC=90°,∴P为三角形BDC的外心,
设△ABC的外心为O,∵△ABC为等边三角形,
∴MO⊥平面ABC,MP⊥平面BDC,
∵二面角A-BC-D的大小为150°,∴∠OPM=60°,
在等边三角形ABC中,由AB=2$\sqrt{3}$,得AP=3,
∴OP=1,在Rt△MOP中,可得MO=$\sqrt{3}$,
在Rt△MOA中,得MA=$\sqrt{A{O}^{2}+M{O}^{2}}=\sqrt{{2}^{2}+(\sqrt{3})^{2}}=\sqrt{7}$.
∴三棱锥A-BCD的外接球的表面积为$4π•(\sqrt{7})^{2}=28π$.
故选:D.
点评 本题考查球的表面积与体积,考查空间想象能力和思维能力,属中档题.

练习册系列答案
相关题目
6.已知集合A={x|x2-3x+2=0},集合B={x|logx4=2},则A∪B=( )
| A. | {-2,1,2} | B. | {-2,2} | C. | {1,2} | D. | {2} |
3.若f′(x0)=-3,则$\underset{lim}{h→0}$$\frac{f({x}_{0}+h)-f({x}_{0}-3h)}{h}$=( )
| A. | -10 | B. | -11 | C. | -12 | D. | -16 |
20.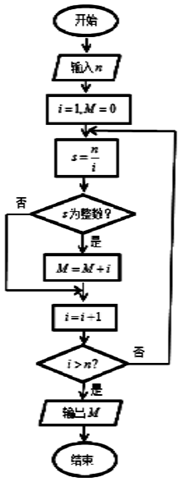 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )| A. | 66 | B. | 65 | C. | 64 | D. | 63 |
7.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
4.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\frac{1}{2}$,则$\overrightarrow{a}$+2$\overrightarrow{b}$与$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
5.已知z是复数,且$\frac{z+2}{i}$=1+i,则z在复平面内对应的点的坐标为( )
| A. | (-3,1) | B. | (-3,-1) | C. | (1,-3) | D. | (-1,-3) |
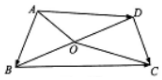 如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.
如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.