题目内容
2.已知抛物线E:y2=4x的焦点为F,圆C:x2+y2-2ax+a2-4=0,直线l与抛物线E交于点A、B两点,与圆C切于点P.(1)当切点P的坐标为($\frac{4}{5}$,$\frac{8}{5}$)时,求直线l及圆C的方程;
(2)当a=2时,证明:|FA|+|FB|-|AB|是定值,并求出该定值.
分析 (1)将P代入圆方程,即可求得a的值,求得圆心,根据直线的斜率公式求得CP的斜率k,则直线l的方程斜率为-$\frac{1}{k}$,利用直线的点斜式方程,即可求得l的方程;
(2)将当l垂直与x轴时,求得A和B点坐标,利用两点之间的斜率公式,即可求得|FA|+|FB|-|AB|的值;当l不垂直于x轴时,由直线l与圆C相切,求得4kb+b2=4,将直线l代入抛物线方程.利用韦达定理及弦长公式求得|AB|,利用抛物线的定义,丨FA丨+丨FB丨=x1+x2+p,即可求得|FA|+|FB|-|AB|是定值.
解答 解:(1)由圆(x-a)2+y2=4,则圆心(a,0),半径为2,
将P($\frac{4}{5}$,$\frac{8}{5}$)代入圆方程,解得:a=2,或a=-$\frac{2}{5}$,
∴圆的方程(x-2)2+y2=4,或(x+$\frac{2}{5}$)2+y2=4,
当a=2,圆心C(2,0)则直线CP的斜率k=$\frac{\frac{8}{5}-0}{\frac{4}{5}-2}$=-$\frac{4}{3}$,
由直线l的斜率为-$\frac{1}{k}$=$\frac{3}{4}$,则直线l的方程y-$\frac{8}{5}$=$\frac{3}{4}$(x-$\frac{4}{5}$),整理得:4y-3x-4=0;
当a=-$\frac{2}{5}$圆心C(-$\frac{2}{5}$,0)则直线CP的斜率k=$\frac{\frac{8}{5}-0}{\frac{4}{5}-(-\frac{2}{5})}$=$\frac{4}{3}$,
由直线l的斜率为-$\frac{1}{k}$=-$\frac{3}{4}$,则直线l的方程y-$\frac{8}{5}$=-$\frac{3}{4}$(x-$\frac{4}{5}$),整理得:20y+15x-44=0,
综上可知:直线l方程:4y-3x-4=0,圆C的方程(x-2)2+y2=4或
直线l方程:20y+15x-44=0,圆C的方程(x+$\frac{2}{5}$)2+y2=4;
(2)当a=2时,圆C的方程(x-2)2+y2=4,
当l垂直与x轴时,则x=4,A(4,4),B(4,-4),
∴丨FA丨=丨FB丨=5,丨AB丨=8,
∴|FA|+|FB|-|AB|=2;
当l不垂直于x轴时,设直线l:y=kx+b(k≠0),
直线l与圆C相切,则$\frac{丨2k-0+b丨}{\sqrt{1+{k}^{2}}}$=2,则4kb+b2=4,
∴b≠0,kb<0,
则$\left\{\begin{array}{l}{y=kx+b}\\{{y}^{2}=4x}\end{array}\right.$,整理得:k2x2+(2kb-4)x+b2=0,
由△=(2kb-4)2-4k2b2=-16kb+4(4kb+b2)=4b2>0,
由x1+x2=-$\frac{2kb-4}{{k}^{2}}$,x1x2=$\frac{{b}^{2}}{{k}^{2}}$,
丨AB丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$•$\sqrt{({-\frac{2kb-4}{{k}^{2}})}^{2}-4×\frac{{b}^{2}}{{k}^{2}}}$=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{-16kb+16}}{{k}^{2}}$,
=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{4{b}^{2}}}{{k}^{2}}$,
=$\frac{\sqrt{4({b}^{2}+{k}^{2}{b}^{2})}}{{k}^{2}}$,
=$\frac{\sqrt{4(4-4kb+{k}^{2}{b}^{2})}}{{k}^{2}}$,
=$\frac{4-2kb}{{k}^{2}}$,
由抛物线的性质可知:丨FA丨+丨FB丨=x1+x2+p=x1+x2+2,
∴|FA|+|FB|=-$\frac{2kb-4}{{k}^{2}}$+2,
∴|FA|+|FB|-|AB|=-$\frac{2kb-4}{{k}^{2}}$+2-$\frac{4-2kb}{{k}^{2}}$=2,
∴|FA|+|FB|-|AB|是定值,定值为2.
点评 本题考查直线与抛物线的位置关系,考查韦达定理,弦长公式及抛物线的焦点弦公式,考查计算能力,属于中档题.

| A. | $y=-\sqrt{x^2}$ | B. | $y=\frac{-x(x-1)}{x-1}$ | ||
| C. | y=-logaax(a>0且a≠1) | D. | $y=-\sqrt{x}•\sqrt{x}$ |

| A. | 2015 | B. | 2016 | C. | 3024 | D. | 1007 |
| A. | $({-∞,\frac{2}{5}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $({-∞,\frac{2}{3}}]$ | D. | (-∞,1] |

| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
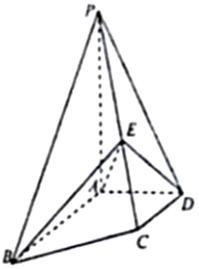 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.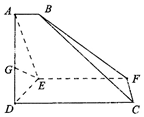 如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.