题目内容
5.已知关于x的方程e2x+ex-a=0有实数解,则实数a的取值范围是( )| A. | [0,+∞) | B. | (0,+∞) | C. | (1,2) | D. | (1,+∞) |
分析 令ex=t>0,则有t2+t-a=0,再根据函数a=${t}^{2}+t=(t+\frac{1}{2})^{2}-\frac{1}{4}$在(0,+∞)上是增函数,求出实数a的取值范围.
解答 解:令ex=t>0,则有t2+t-a=0,化简可得a=${t}^{2}+t=(t+\frac{1}{2})^{2}-\frac{1}{4}$.
∴函数a=${t}^{2}+t=(t+\frac{1}{2})^{2}-\frac{1}{4}$在(0,+∞)上是增函数,故a>0.
∴a的取值范围为(0,+∞).
故选:B.
点评 本题考查根的存在性与根的个数的判定,训练了换元法与配方法求二次函数的最值,是基础题.

练习册系列答案
相关题目
13.某程序框图如图所示,该程序运行后输出的S的值是( )


| A. | 2015 | B. | 2016 | C. | 3024 | D. | 1007 |
17.在数列{an}中,已知a1=3,且数列{an+(-1)n}是公比为2的等比数列,对于任意的n∈N*,不等式a1+a2+…+an≥λan+1恒成立,则实数λ的取值范围是( )
| A. | $({-∞,\frac{2}{5}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $({-∞,\frac{2}{3}}]$ | D. | (-∞,1] |
15.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1536石,验得米内夹谷,抽样取米一把,数得224粒内夹谷28粒,则这批米内夹谷约为( )
| A. | 169石 | B. | 192石 | C. | 1367石 | D. | 1164石 |
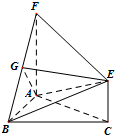 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.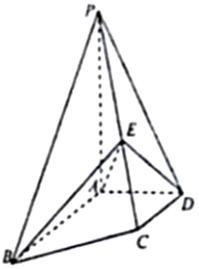 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.