题目内容
17．100张卡片上分别写有1，2，3，…，100，从中任取1张，则这张卡片上的数是6的倍数的概率是$\frac{4}{25}$．分析 在100张卡片上分别写上1至100这100个数字，从中任取一张共有100种取法，其中所得卡片上的数字为6的倍数的数是6，12，…，96，可得出满足条件的数据的个数，再利用古典概型的概率计算公式即可得出．
解答 解：在100张卡片上分别写上1至100这100个数字，从中任取一张共有100种取法，
其中所得卡片上的数字为6的倍数的数是：
6，12，18，24，30，36，42，48，54，60，66，72，78，84，90，96共16个，
∴所得卡片上的数字为6的倍数的数共有16个．
∴所得卡片上的数字为6的倍数的概率P=$\frac{16}{100}$=$\frac{4}{25}$，
故答案为：$\frac{4}{25}$．
点评 本题考查了古典概型的概率计算公式和等差数列的通项公式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
7．设M、N是直线x+y-2=0上的两动点，且|MN|=$\sqrt{2}$，则$\overrightarrow{OM}$•$\overrightarrow{ON}$的最小值为（ ）
| A． | 1 | B． | 2 | C． | $\frac{5}{2}$ | D． | $\frac{3}{2}$ |
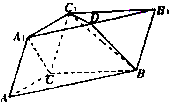在三棱柱ABC-A1B1C1中，AC=BC=2，∠ACB=120°，D为A1B1的中点．
5．设集合A={x|x2-3x＜0}，B={x||x|＞2}，则A∩B=（ ）
| A． | （2，3） | B． | （-2，3） | C． | （0，2） | D． | （-2，0） |
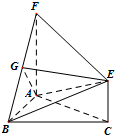如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF$\stackrel{∥}{=}$2CE，G是线段BF上一点，AB=AF=BC．
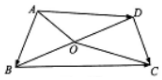如图，在平面四边形ABCD中，O为BD的中点，且OA=3，OC=5，若$\overrightarrow{AB}$•$\overline{AD}$=-7，则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9．
9．下列函数中哪个与函数y=-x相等（ ）
| A． | $y=-\sqrt{x^2}$ | B． | $y=\frac{-x（x-1）}{x-1}$ | ||
| C． | y=-logaax（a＞0且a≠1） | D． | $y=-\sqrt{x}•\sqrt{x}$ |
6．对任意x∈[0，$\frac{π}{6}$]，任意y∈（0，+∞），不等式$\frac{y}{4}$-2cos2x≥asinx-$\frac{9}{y}$恒成立，则实数a的取值范围是（ ）
| A． | （-∞，3] | B． | [-2$\sqrt{2}$，3] | C． | [-2$\sqrt{2}$，2$\sqrt{2}$] | D． | [-3，3] |