题目内容
10.已知f(x)=$\frac{{a}^{x}-1}{{a}^{x}+1}$(a>0,a≠1).(Ⅰ)判断f(x)的奇偶性;
(Ⅱ)求使f(x)>$\frac{1}{2}$的x取值范围.
分析 (Ⅰ)利用奇函数的定义,判断f(x)的奇偶性;
(Ⅱ)f(x)>$\frac{1}{2}$,即$\frac{{a}^{x}-1}{{a}^{x}+1}$>$\frac{1}{2}$,分类讨论,即可求使f(x)>$\frac{1}{2}$的x取值范围.
解答 解:(Ⅰ)f(-x)=$\frac{{a}^{-x}-1}{{a}^{-x}+1}$=-$\frac{{a}^{x}-1}{{a}^{x}+1}$=-f(x)
∴f(x)是奇函数;
(Ⅱ)f(x)>$\frac{1}{2}$,即$\frac{{a}^{x}-1}{{a}^{x}+1}$>$\frac{1}{2}$,
∴ax>3,
则a>1,可得x>loga3;0<a<1,可得x<loga3.
点评 本题考查函数的奇偶性,考查学生解不等式的能力,比较基础.

练习册系列答案
相关题目
20.一元二次不等式-x2+4x+5<0的解集为( )
| A. | (-1,5) | B. | (-5,1) | C. | (-∞,-1)∪(5,+∞) | D. | (-∞,-5)∪(1,+∞) |
1.调查某桑场采桑员和辅助工关于桑毛虫皮炎发病情况结果如表:
(1)完成2×2列联表;
(2)利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?
(参考公式:χ2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 |
(2)利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?
| 参考数据 | 当χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当χ2>6.635时,有99%把握判定变量A,B有关联. |
5.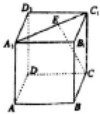 如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )
如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )
 如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )
如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )| A. | AC | B. | BD | C. | A1D | D. | A1D1 |
2.有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次,根据年龄将大众评委分为5组,各组的人数如表:
(1)为了调查评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从E组中抽取了8人.请将其余各组抽取的人数填入如表.
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,设每位评委支持歌手不相互影响,求这2人至少有1人支持1号歌手的概率.
| 组别 | A | B | C | D | E |
| 人数 | 50 | 50 | 150 | 150 | 100 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 50 | 150 | 150 | 100 |
| 抽取人数 | 8 |
19.等比数列-3,-6,…的第四项等于( )
| A. | -24 | B. | -9 | C. | -12 | D. | 24 |
14.已知函数y=x3-ax2-3x+b在x=1处取得极值2,则实数a,b的值分别为( )
| A. | 0和-4 | B. | 0;b取任意实数 | C. | 0和4 | D. | 4;b取任意实数 |