题目内容
5.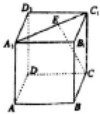 如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )
如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )| A. | AC | B. | BD | C. | A1D | D. | A1D1 |
分析 由线面垂直的判定能推导出BD⊥平面A1C1C,根据线面垂直的性质从而可得BD⊥CE,从而得解.
解答  解:∵在正方体ABCD-A1B1C1D1中,ABCD是正方形,
解:∵在正方体ABCD-A1B1C1D1中,ABCD是正方形,
∴BD⊥A1C1,且BD⊥CC1,又A1C1∩CC1=C1,
∴BD⊥平面A1C1C,
又∵CE?平面A1C1C,
∴BD⊥CE,
故选:B.
点评 本题主要考查了线面垂直的判定及性质,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.下列函数中,最小正周期为$\frac{π}{2}$的是( )
| A. | y=sin$\frac{x}{2}$ | B. | y=2sinx | C. | y=sin4π | D. | y=sin(-4x) |
20.已知定义在[-1,+∞]上的函数在区间[-1,3)上的解析式为f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}}(-1≤x<1)}\\{\frac{3}{2}-\frac{3}{x}×|x-2|(1≤x<3)}\end{array}\right.$,当x≥3时,函数满足f(x)=f(x-4)+1,若函数g(x)=f(x)-kx-k有6个零点,则实数k的取值或取值范围为( )
| A. | ($\frac{5}{14}$,$\frac{9+\sqrt{21}}{40}$) | B. | $\frac{5}{14}$ | C. | ($\frac{5}{12}$,$\frac{1}{2}$) | D. | ($\frac{5}{14}$,$\frac{5}{12}$) |
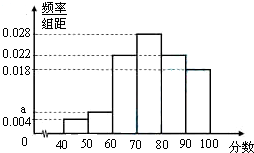 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]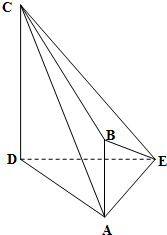 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.