题目内容
20.一元二次不等式-x2+4x+5<0的解集为( )| A. | (-1,5) | B. | (-5,1) | C. | (-∞,-1)∪(5,+∞) | D. | (-∞,-5)∪(1,+∞) |
分析 要解的不等式即即 x2-4x-5>0,即 (x-5)(x+1)>0,由此求得x的范围.
解答 解:一元二次不等式-x2+4x+5<0,即 x2-4x-5>0,即 (x-5)(x+1)>0,
∴x<-1,或x>5,
故选:C.
点评 本题主要考查一元二次不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
8.数列{an}满足a1=1,且对任意的n∈N*都有an+1=an+n+1,则数列{$\frac{1}{a_n}}$}的 前100项的和为( )
| A. | $\frac{101}{100}$ | B. | $\frac{200}{101}$ | C. | $\frac{99}{100}$ | D. | $\frac{101}{200}$ |
12.当a<0时,函数y=$\frac{1}{3}$x3-ax2-3a2x-4在(2,+∞)上是增函数,则实数a的取值范围是( )
| A. | (-2,0) | B. | [-2,0) | C. | [-2,1] | D. | (-2,1] |
9.函数y=sinx+$\sqrt{3}$cosx的最小值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | -2 |

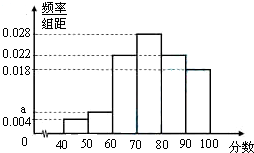 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]