题目内容

已知向量
a
=（1-x，1-x，x），
b
=（2，x，x）（x∈R），则|
a
-
b
|的最小值是
 
．
考点：平面向量数量积的运算
专题：计算题,空间向量及应用
分析：运用向量的加减运算和向量模的公式，再由二次函数的最值求法，即可计算得到．
解答： 解：由于向量
a
=（1-x，1-x，x），
b
=（2，x，x），
则
a
-
b
=（-1-x，1-2x，0），
则|
a
-
b
|=
(-1-x)2+(1-2x)2
=
5x2-2x+2
=
5(x-
1
5
)2+
9
5
，
当x=
1
5
时，取得最小值
3
5
5
．
故答案为：
3
5
5
点评：本题考查空间向量及运用，考查向量的加减和模的运算，考查二次函数的最值，属于基础题．
练习册系列答案
相关题目
已知双曲线
y2
a2
-
x2
b2
=1（a＞0，b＞0）的离心率e=
2
3
3
，
（1）求双曲线的渐近线方程；
（2）若原点到直线
x
a
-
y
b
=1的距离为
3
2
，求曲线的方程式．
已知函数f（x）=（2x+1）ln（2x+1）-a（2x+1）2-x（a＞0）．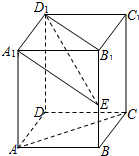
（1）若函数f（x）在x=0处取极值，求a的值；
（2）如图，设直线x=-
1
2
，y=-x将坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域（不含边界），若函数y=f（x）的图象恰好位于其中一个区域内，判断其所在的区域并求对应的a的取值范围；
（3）比较32×43×54×…×20142013与23×34×45×…×20132014的大小，并说明理由．
如图，在直四棱柱ABCD-A1B1C1D1中，底面是边长为
2
的正方形，AA1=3，点E在棱B1B上运动．
（Ⅰ）证明：AC⊥D1E；
（Ⅱ）若三棱锥B1-A1D1E的体积为
2
3
时，求异面直线AD，D1E所成的角．
如果向量
a
与
b
的夹角为θ，定义
a
×
b
为向量
a
与
b
的“向量积”：
a
×
b
是一个向量，其长度为|
a
×
b
|=|
a
||
b
|sinθ，如果|
a
|=5，|
b
|=1，
a
•
b
=-3，则|
a
×
b
|的值为
 
．
用符号“＞”或“＜”填空：
（1）0.92
 
0.96；
（2）1.70.3
 
1.70.4；
（3）0.9-1
 
0.9-1．
直线l：y=
3
（x-2）和双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）交于A，B两点，且|AB|=
3
，又l关于直线l1：y=
b
a
x对称的直线l2与x轴平行．
（1）求双曲线C的离心率；
（2）求双曲线C的方程．
在△ABC中，A为动点，B、C为定点，B（-
a
2
，0），C（
a
2
，0）（a＞0），且满足条件sinC-sinB=
1
2
sinA，则动点A的轨迹方程是
 
．
已知向量
a
=（sin2x，
3
），b=（1，-cos2x），x∈R．
（1）若
a
⊥
b
，且0＜x＜
π
2
，求x的值；
（2）求函数f（x）=
a
•
b
的单调增区间（结果用开区间表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网