题目内容
在数列{an}中,如果存在非零的常数T,使an+T=an,对于任意正整数n均成立,就称数列{an}为周期函数,其中T叫做数列{an}的周期.已知数列{xn}满足xn+2=|xn+1-xn|(x∈N*),x1=1,x2=a.
①若a=0,则数列{xn}的周期为3.
②若数列{xn}的周期为3,则a=0.
③若数列{an}的前n项和为Sn,且周期为3,则S3n=2n(n为常数)
④若a=3,则数列{xn}的周期为4;
⑤若a=2,则数列{xn}前2014项的和为1345.
则这五个命题中真命题是 .
①若a=0,则数列{xn}的周期为3.
②若数列{xn}的周期为3,则a=0.
③若数列{an}的前n项和为Sn,且周期为3,则S3n=2n(n为常数)
④若a=3,则数列{xn}的周期为4;
⑤若a=2,则数列{xn}前2014项的和为1345.
则这五个命题中真命题是
考点:命题的真假判断与应用
专题:函数的性质及应用,点列、递归数列与数学归纳法
分析:利用x1=1,x2=a,xn+2=|xn+1-xn|(x∈N*),对①②③④⑤五个选项逐一判断即可得到答案.
解答:
解:∵x1=1,x2=a,xn+2=|xn+1-xn|,
∴x3=|a-1|,
①若a=0,则x3=|0-1|=1,又数列{xn}的周期为3,
∴x4=|x3-x2|=|1-0|=x1=1,
同理可求x5=0,x6=1,
∴数列{xn}为1,0,1,1,0,1,1,0,1,…
∴数列{xn}的周期为3,正确;
②∵x1=1,x2=a,xn+2=|xn+1-xn|,
∴x3=|a-1|,又数列{xn}的周期为3,
∴x4=|x3-x2|=||a-1|-a|=x1=1,
解得:a=1或a=0,故②错误;
③由②知a=1或a=0,
若a=0,由①知,数列{xn}为1,0,1,1,0,1,1,0,1,…,
∴x1+x2+x3=x4+x5+x6=x7+x8+x9=…=x3n-2+x3n-1+x3n=2,
∴S3n=2n;
若a=1,则x1=x3n-2=1,x2=x3n-1=1,x3=x3n=0,
∴S3n=2n;
综上所述,S3n=2n,故③正确;
④若a=3,则x2=a=3,x3=|x2-x1|=|3-1|=2,x4=|x3-x2|=|2-3|=1,
同理可求x5=1,x6=0,x1≠x5,故④错误;
⑤若a=2,则x2=a=2,x3=|x2-x1|=|2-1|=1,x4=|x3-x2|=|1-2|=1,
同理可求x5=0,x6=1,x7=1,x8=0…,
从第四项起,为1,0,1,1,0,1,1,0,1,…函数值周期出现,连续三项之和为2;
∵2014=671×3+1,
∴数列{xn}前2014项的和为:(x1+x2+x3)+670×2+1=1+2+1+1340+1=1345,故⑤正确.
综上所述,五个命题中真命题是①③⑤.
故答案为:①③⑤.
∴x3=|a-1|,
①若a=0,则x3=|0-1|=1,又数列{xn}的周期为3,
∴x4=|x3-x2|=|1-0|=x1=1,
同理可求x5=0,x6=1,
∴数列{xn}为1,0,1,1,0,1,1,0,1,…
∴数列{xn}的周期为3,正确;
②∵x1=1,x2=a,xn+2=|xn+1-xn|,
∴x3=|a-1|,又数列{xn}的周期为3,
∴x4=|x3-x2|=||a-1|-a|=x1=1,
解得:a=1或a=0,故②错误;
③由②知a=1或a=0,
若a=0,由①知,数列{xn}为1,0,1,1,0,1,1,0,1,…,
∴x1+x2+x3=x4+x5+x6=x7+x8+x9=…=x3n-2+x3n-1+x3n=2,
∴S3n=2n;
若a=1,则x1=x3n-2=1,x2=x3n-1=1,x3=x3n=0,
∴S3n=2n;
综上所述,S3n=2n,故③正确;
④若a=3,则x2=a=3,x3=|x2-x1|=|3-1|=2,x4=|x3-x2|=|2-3|=1,
同理可求x5=1,x6=0,x1≠x5,故④错误;
⑤若a=2,则x2=a=2,x3=|x2-x1|=|2-1|=1,x4=|x3-x2|=|1-2|=1,
同理可求x5=0,x6=1,x7=1,x8=0…,
从第四项起,为1,0,1,1,0,1,1,0,1,…函数值周期出现,连续三项之和为2;
∵2014=671×3+1,
∴数列{xn}前2014项的和为:(x1+x2+x3)+670×2+1=1+2+1+1340+1=1345,故⑤正确.
综上所述,五个命题中真命题是①③⑤.
故答案为:①③⑤.
点评:本题考查命题的真假判断与应用,着重考查函数的周期性与数列的求和,考查分类讨论思想、综合运算能力与推理能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
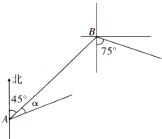 在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.(注:n mile是海里的英文符号)
在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.(注:n mile是海里的英文符号)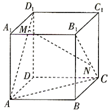 如图,棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是线段AD1和B1C上的动点,且满足D1M=CN,则下列命题正确的是
如图,棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是线段AD1和B1C上的动点,且满足D1M=CN,则下列命题正确的是