题目内容
在△ABC中,若AB=4,BC=2
,且
•
=-8,则AC= .
| 2 |
| BA |
| BC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用
=
-
,可得
2=
2+
2-2
•
即可得出.
| AC |
| BC |
| BA |
| AC |
| BC |
| BA |
| BC |
| BA |
解答:
解:∵|
|=4,|
|=2
,且
•
=-8,
=
-
,
∴
2=
2+
2-2
•
=(2
)2+42-2×(-8)=40,
∴|
|=2
.
故答案为:2
.
| BA |
| BC |
| 2 |
| BA |
| BC |
| AC |
| BC |
| BA |
∴
| AC |
| BC |
| BA |
| BC |
| BA |
| 2 |
∴|
| AC |
| 10 |
故答案为:2
| 10 |
点评:本题考查了向量的三角形法则、数量积的性质,属于基础题.

练习册系列答案
相关题目
设a>b,c>d,则下列不等式一定正确的是( )
| A、a+c>b+d | ||||
| B、ac>bd | ||||
C、
| ||||
| D、a-c>b-d |
已知f(x)=cos(ωx+
)的图象与y=1的图象的两相邻交点间的距离为π,要得到y=f(x)的图象,只需把y=sinωx的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
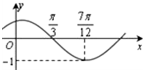 函数f(x)=Asin(ωx+φ)的图象如图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象向右平移
函数f(x)=Asin(ωx+φ)的图象如图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象向右平移