题目内容
已知点M(1,A),N(4,-A)是函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
<φ<
)一个周期内图象上的两点,函数f(x)的图象与y轴交于点P,满足
•
=1.
(Ⅰ)求f(x)的表达式;
(Ⅱ)求函数y=f(x)-
在区间[0,6]内的零点.
| π |
| 2 |
| π |
| 2 |
| PM |
| PN |
(Ⅰ)求f(x)的表达式;
(Ⅱ)求函数y=f(x)-
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)由题意求出函数周期,代入周期公式求得ω的值,再由f(1)=A结合φ的范围求得φ值,由x为0求出P的坐标,结合
•
=1求得A的值,则f(x)的表达式可求;
(Ⅱ)把f(x)的解析式代入y=f(x)-
,整理后由y=0直接求解在区间[0,6]内x的值.
| PM |
| PN |
(Ⅱ)把f(x)的解析式代入y=f(x)-
| 3 |
解答:
解:(I)∵点M(1,A),N(4,-A)是函数f(x)=Asin(ωx+φ)一个周期内图象上的两点,
∴
=4-1=3,T=
=6,ω=
;
由f(1)=A,得Asin(
+φ)=A,∴sin(
+φ)=1,
又-
<φ<
,∴φ=
;
又f(0)=Asin
=
,∴P(0,
),
∴
=(1,
),
=(4,-
A),
由
•
=1,得4-
A2=1,∴A=2.
∴f(x)=2sin(
x+
);
(II)∵x∈[0,6],∴
x+
∈[
,
],
∴y=f(x)-
=2sin(
x+
)-
,
由y=0,得sin(
x+
)=
,
∴
x+
=
或
x+
=
,
得x=
或x=
.
∴函数y=f(x)-
在区间[0,6]内的零点为
,
.
∴
| T |
| 2 |
| 2π |
| ω |
| π |
| 3 |
由f(1)=A,得Asin(
| π |
| 3 |
| π |
| 3 |
又-
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
又f(0)=Asin
| π |
| 6 |
| A |
| 2 |
| A |
| 2 |
∴
| PM |
| A |
| 2 |
| PN |
| 3 |
| 2 |
由
| PM |
| PN |
| 3 |
| 4 |
∴f(x)=2sin(
| π |
| 3 |
| π |
| 6 |
(II)∵x∈[0,6],∴
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |
∴y=f(x)-
| 3 |
| π |
| 3 |
| π |
| 6 |
| 3 |
由y=0,得sin(
| π |
| 3 |
| π |
| 6 |
| ||
| 2 |
∴
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
得x=
| 1 |
| 2 |
| 3 |
| 2 |
∴函数y=f(x)-
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了函数y=Asin(ωx+φ)的图象变换,考查了函数解析式的求法,训练了函数零点的求解方法,解答此题的关键是由题意得到周期,是中档题.

练习册系列答案
相关题目
曲线y=
ex在点(2,
e2)处的切线与坐标轴所围三角形的面积为( )
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||
| B、4e2 | ||
| C、2e2 | ||
D、
|
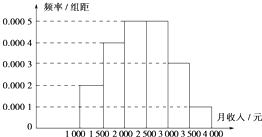 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)):
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)):