题目内容
已知f（x）=cos(ωx+
)的图象与y=1的图象的两相邻交点间的距离为π，要得到y=f（x）的图象，只需把y=sinωx的图象（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：计算题,三角函数的图像与性质
分析：依题意，可知函数y=f（x）的周期T=
=π，从而可求ω，利用诱导公式将f（x）=cos（2x+
）转化为正弦关系式，再由函数y=Asin（ωx+φ）的图象变换可得答案．
| 2π |
| ω |
| π |
| 3 |
解答：
解：∵f（x）=cos（ωx+
）的最大值为1，其图象与y=1的图象的两相邻交点间的距离为π，令ω＞0，
∴函数y=f（x）的周期T=
=π，
∴ω=2；
∴f（x）=cos（2x+
）=sin[（2x+
）+
]=sin2（x+
），
∴要得到y=f（x）的图象，只需把y=sin2x的图象向左移动
个单位长度单位，
故选：A．
| π |
| 3 |
∴函数y=f（x）的周期T=
| 2π |
| ω |
∴ω=2；
∴f（x）=cos（2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
∴要得到y=f（x）的图象，只需把y=sin2x的图象向左移动
| 5π |
| 12 |
故选：A．
点评：本题考查函数y=Asin（ωx+φ）的图象变换，利用诱导公式将f（x）=cos（2x+
）转化为正弦关系式f（x）=sin2（x+
）是关键，考查转化思想与运算能力，属于中档题．
| π |
| 3 |
| 5π |
| 12 |
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=（cosx-m）2+1在cosx=-1时取得最大值，在cosx=m时取得最小值，则实数m的取值范围是（ ）
| A、m≤-1 | B、m≥1 |
| C、0≤m≤1 | D、-1≤m≤0 |
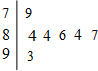如图是2013年某大学自主招生面试环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和众数依次为（ ）| A、85，84 |
| B、84，85 |
| C、86，84 |
| D、84，86 |
函数y=cos2(x+
)-cos2(x-
)是（ ）
| π |
| 4 |
| π |
| 4 |
| A、最小正周期为π的偶函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为π的奇函数 |
对一个样本容量为100的数据分组，各组的频数如表：
估计小于29的数据大约占总体的（ ）
| 区间 | [17，19） | [19，21） | [21，23） | [23，25） | [25，27） | [27，29） | [29，31） | [31，33] |
| 频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
| A、42% | B、58% |
| C、40% | D、16% |
将函数y=cos(2x-
π)的图象向左平移φ（φ＞0）个单位，所得图象关于y轴对称，则φ的最小值为（ ）
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|