题目内容
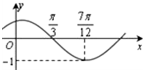 函数f(x)=Asin(ωx+φ)的图象如图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象向右平移
函数f(x)=Asin(ωx+φ)的图象如图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象向右平移考点:函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:由图知,A=1,令ω>0,易求ω=2,由
×2+φ=2kπ+π(k∈Z)可求得φ=2kπ+
(k∈Z),于是可得f(x)=sin(2x+
),为了得到g(x)=-cos2x的图象,利用函数y=Asin(ωx+φ)的图象变换即可求得答案.
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答:
解:由图知,A=1,
=
-
=
,令ω>0,
则T=
=π,
∴ω=2,
又
×2+φ=2kπ+π(k∈Z),
∴φ=2kπ+
(k∈Z),
∴f(x)=sin(2x+
),
∵g(x)=-cos2x=sin(2x-
),
f(x-
)=sin[2(x-
)+
]=sin(2x-
)=g(x),
∴要得到g(x)=-cos2x=sin(2x-
)的图象,可以将f(x)的图象向右平移
个单位长度,
故答案为:
.
| T |
| 4 |
| 7π |
| 12 |
| π |
| 3 |
| π |
| 4 |
则T=
| 2π |
| ω |
∴ω=2,
又
| π |
| 3 |
∴φ=2kπ+
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
∵g(x)=-cos2x=sin(2x-
| π |
| 2 |
f(x-
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
∴要得到g(x)=-cos2x=sin(2x-
| π |
| 2 |
| 5π |
| 12 |
故答案为:
| 5π |
| 12 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查运算求解能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
把函数y=sin2x的图象向左平移
个单位长度,再把所得图象所有点的横坐标伸长到原来的2倍(纵坐标不变),所得函数图象的解析式为( )
| π |
| 4 |
| A、y=sinx | ||
| B、y=cosx | ||
C、y=sin(x+
| ||
| D、y=-sinx |
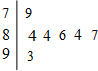 如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )| A、85,84 |
| B、84,85 |
| C、86,84 |
| D、84,86 |