题目内容
设a>b,c>d,则下列不等式一定正确的是( )
| A、a+c>b+d | ||||
| B、ac>bd | ||||
C、
| ||||
| D、a-c>b-d |
考点:不等关系与不等式
专题:不等式的解法及应用
分析:由条件利用由不等式的性质可得 a+c>b+d,从而得出结论.
解答:
解:∵a>b,c>d,由不等式的性质可得 a+c>b+d,故A正确,
不妨令a=2、b=1、c=-1、d=-2,
显然,ac=bd=-2,故B不正确;
=-2,
=
,
<
,故C不正确;
a-c=b-d=3,故D不正确.
故选:A.
不妨令a=2、b=1、c=-1、d=-2,
显然,ac=bd=-2,故B不正确;
| a |
| c |
| b |
| d |
| 1 |
| -2 |
| a |
| c |
| b |
| d |
a-c=b-d=3,故D不正确.
故选:A.
点评:本题主要考查不等式与不等关系,不等式性质的应用,属于基础题.

练习册系列答案
相关题目
把函数y=sin2x的图象向左平移
个单位长度,再把所得图象所有点的横坐标伸长到原来的2倍(纵坐标不变),所得函数图象的解析式为( )
| π |
| 4 |
| A、y=sinx | ||
| B、y=cosx | ||
C、y=sin(x+
| ||
| D、y=-sinx |
在△ABC中a、b、c分别是角A、B、C的对边,
=
,角A=( )
| tanA |
| tanB |
| ||
| b |
| A、30° | B、45° |
| C、60° | D、90° |
函数f(x)=cos(2x+
),下列关于该函数的叙述正确的是( )
| π |
| 3 |
| A、f(x)的最小正周期为2π | ||
B、f(x)的图象可以由y=sin2x向左平移
| ||
C、f(x)图象关于直线x=
| ||
D、函数f(x)在区间(0,
|
已知函数f(x)=(cosx-m)2+1在cosx=-1时取得最大值,在cosx=m时取得最小值,则实数m的取值范围是( )
| A、m≤-1 | B、m≥1 |
| C、0≤m≤1 | D、-1≤m≤0 |
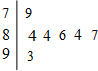 如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )| A、85,84 |
| B、84,85 |
| C、86,84 |
| D、84,86 |