题目内容
数列{an}的前n项和Sn=n2-2n，则a4等于（ ）
| A、-7 | B、-1 | C、0 | D、1 |
考点：数列的函数特性
专题：等差数列与等比数列
分析：由Sn=n2-2n，可得a4=S4-S3，从而可得答案．
解答：
解：∵Sn=n2-2n，
∴a4=S4-S3=42-24-（32-23）=-1．
故选：B．
∴a4=S4-S3=42-24-（32-23）=-1．
故选：B．
点评：本题考查数列的递推关系的应用，依题意得a4=S4-S3是关键，属于基础题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
下列函数与y=-x是同一函数的是（ ）
A、y=-
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
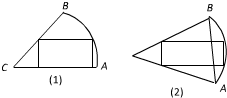某工厂生产主要产品后，留下大量中心角为60°，半径为a的扇形边角料，现要废物利用，从中剪裁出矩形毛坯，要求矩形面积尽可能大，并如图设计了两种裁剪方法，一种是使矩形的一边落在扇形的半径上，另一种是使矩形的两顶点分别在扇形的两条半径上，请选出最佳方案．已知等差数列{an}的前n项和为Sn，且满足
-
=1，则数列{an}的公差是（ ）
| S4 |
| 4 |
| S3 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |