题目内容
3.在椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$中,满足a2+b2-3c2=0,c是半焦距,则$\frac{a+c}{a-c}$=( )| A. | $3+2\sqrt{2}$ | B. | $3+\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | $2+2\sqrt{2}$ |
分析 利用a2=b2+c2及a2+b2-3c2=0求出a、c的数量关系即可.
解答 解:由a2=b2+c2及a2+b2-3c2=0 得a2=2c2⇒a=$\sqrt{2}c$,则$\frac{a+c}{a-c}$=$\frac{\sqrt{2}+1}{\sqrt{2}-1}=3+2\sqrt{2}$,
故选:A.
点评 本题考查了椭圆中a2=b2+c2的应用,是基础题.

练习册系列答案
相关题目
18.设x,y满足$\left\{\begin{array}{l}2x+y≤4\\ x-y≥-1\\ x+2y≥2\end{array}\right.$,则z=x-3y的最小值为( )
| A. | -2 | B. | -4 | C. | -5 | D. | -3 |
12.已知函数f(x)=ax3-3x的图象过点(-1,4),则实数a=( )
| A. | -2 | B. | 1 | C. | -1 | D. | 2 |
13.已知集合A={0,4,5},B={0,1,2},U={0,1,2,3,4,5},则(∁UA)∩B=( )
| A. | {1,2} | B. | {3} | C. | {0} | D. | {0,1,2,3} |
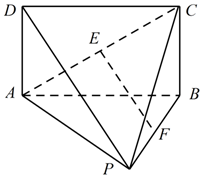 如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.
如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.