题目内容

18．设x，y满足$\left\{\begin{array}{l}2x+y≤4\\ x-y≥-1\\ x+2y≥2\end{array}\right.$，则z=x-3y的最小值为（　　）
A．-2B．-4C．-5D．-3

分析 画出约束条件的可行域，利用目标函数的几何意义，求解最小值即可．

解答 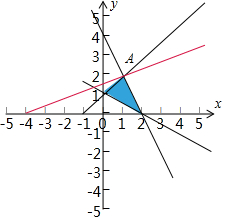解：x，y满足$\left\{\begin{array}{l}2x+y≤4\\ x-y≥-1\\ x+2y≥2\end{array}\right.$，的可行域如图：
z=x-3y即：y=$\frac{1}{3}$x-$\frac{1}{3}$z，z=x-3y的最小值就是直线在y轴上的截距最大时，显然经过A时z最小．
由$\left\{\begin{array}{l}{2x+y=4}\\{x-y=-1}\end{array}\right.$，可得A（1，2）．
z的最小值为：1-6=-5．
故选：C．

点评 本题主要考查线性规划的应用，利用z的几何意义，通过数形结合是解决本题的关键．

练习册系列答案
相关题目
15．根据下列条件，解三角形．
（Ⅰ）已知 b=4，c=8，B=30°，求C，A，a；
（Ⅱ）在△ABC中，B=45°，C=75°，b=2，求a，c，A．
9．已知函数y=f（x2-2x）在区间（-∞，-1]上单调递增，在区间[1，3]上是减函数，则y=f（x）（　　）
A．在区间（-∞，3]上递增B．在区间（-∞，-1]上递增
C．在区间（-∞，3]上递减D．在区间（-∞，-1]上递减
6．下列函数中，既是奇函数又在区间（0．+∞）上单调递增的函数是（　　）
A．y=1nxB．y=x3C．y=2|x |D．y=-x
13．已知函数f（x）=$\left\{\begin{array}{l}ax+b，x＜0\\{2^x}，x≥0\end{array}\right.$，且f（-2）=3，f（-1）=f（1）．
（Ⅰ）求f（x）的解析式，并求f（f（-2））的值；
（Ⅱ）请在给定的直角坐标系内，利用“描点法”画出y=f（x）的大致图象．
3．在椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$中，满足a2+b2-3c2=0，c是半焦距，则$\frac{a+c}{a-c}$=（　　）
A．$3+2\sqrt{2}$B．$3+\sqrt{2}$C．$2+\sqrt{2}$D．$2+2\sqrt{2}$
10．已知lnx+1≤x（x＞0），则$\frac{{{x^2}-1nx+x}}{x}（x＞0）$的最小值为1．
7．已知椭圆Γ：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左顶点为A，右焦点为F2，过点F2作垂直于x轴的直线交该椭圆于M、N两点，直线AM的斜率为$\frac{1}{2}$．
（1）求椭圆Γ的离心率；
（2）若△AMN的外接圆在点M处的切线与椭圆交于另一点D，△F2MD的面积为$\frac{6}{7}$，求椭圆Γ的标准方程．
8．若函数f（x）的定义域为[1，2]，则函数y=f（x2）的定义域为（　　）
A．[1，4]B．[1，$\sqrt{2}$]C．[-$\sqrt{2}$，$\sqrt{2}$]D．[-$\sqrt{2}$，-1]∪[1，$\sqrt{2}$]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网