题目内容
6.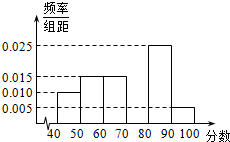 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:(1)求第四小组的频率,补全这个频率分布直方图;并估计该校学生的数学成绩的中位数.(精确到0.1);
(2)按分层抽样的方法在数学成绩是[60,70),[70,80)的两组学生中选6人,再在这6人种任取两人,求他们的分数在同一组的概率;
(3)若从全市参加高一年级期末考试的学生中,任意抽取3个学生,设这3个学生中数学成绩为80分以上(包括80分)的人数为X,(以该校学生的成绩的频率估计概率),求X的数学期望.
分析 (1)由各组的频率和等于1,能求出第四组的频率,并能作出频率直方图.
(2)按分层抽样的方法从中选6人,则数学成绩是[60,70)的学生中选2人,数学成绩是[70,80)的学生中选4人,由此能求出他们的分数在同一组的概率.
(3)由频率分布直方图得数学成绩为80分以上(包括80分)的概率为0.3,任意抽取3个学生,设这3个学生中数学成绩为80分以上(包括80分)的人数为X,则X~B(3,0.3),由此能求出X的数学期望.
解答  解:(1)∵各组的频率和等于1,
解:(1)∵各组的频率和等于1,
∴第四组的频率:f4=1-(0.025+0.015×2+0.01+0.005)×10=0.3,
作出频率直方图如右图:
(2)数学成绩是[60,70)的学生数所占频率为0.15,数学成绩是[70,80)的学生所点频率为0.3,
按分层抽样的方法从中选6人,则数学成绩是[60,70)的学生中选2人,数学成绩是[70,80)的学生中选4人,
从这6人中任取两人,基本事件总数n=${C}_{6}^{2}$=15,
他们的分数在同一组包含的基本事件个数m=${C}_{2}^{2}+{C}_{4}^{2}$=7,
∴他们的分数在同一组的概率p=$\frac{m}{n}$=$\frac{7}{15}$.
(3)由频率分布直方图得数学成绩为80分以上(包括80分)的概率为0.3,
任意抽取3个学生,设这3个学生中数学成绩为80分以上(包括80分)的人数为X,则X~B(3,0.3),
P(X=0)=${C}_{3}^{0}0.{7}^{3}$=0.343,
P(X=1)=${C}_{3}^{1}0.3•0.{7}^{2}$=0.441,
P(X=2)=${C}_{3}^{2}0.{3}^{2}•0.7$=0.189,
P(X=3)=${C}_{3}^{3}0.{3}^{3}$=0.027,
∴X的数学期望EX=3×0.3=0.9.
点评 本题考查频率分布直方图的应用,考查概率的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

| A. | $\frac{2}{11}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{11}{2}$ |
| A. | {-1,2} | B. | {-2,-1,1,2,4} | C. | {1,4} | D. | ∅ |
| A. | {x|0<x<4} | B. | {x|1<x<7} | C. | {x|1<x<4} | D. | {x|4<x<7} |
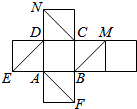 如图是正方体的平面展开图,则在这个正方体中
如图是正方体的平面展开图,则在这个正方体中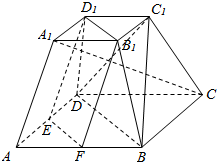 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.