题目内容
9.下列说法中①命题“每个指数函数都是单调函数”是全称命题,而且是真命题;
②若m?α,n?α,m,n是异面直线,那么n与α相交;
③设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=2a(a>0),则动点P的轨迹是椭圆;
④若实数k满足0<k<9,则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1有相同的焦点.
其中正确的为①④.(写出所有真命题的序号)
分析 由指数函数的图象和性质,可判断①;由直线与平面位置关系的几何特征,可判断②;根据椭圆的定义,可判断③;根据双曲线的简单性质,可判断④.
解答 解:①命题“每个指数函数都是单调函数”可化为:“?函数f(x)=ax,(a>0,且a≠1),f(x)为单调函数”,是全称命题,而且是真命题,故正确;
②若m?α,n?α,m,n是异面直线,那么n与α相交,或n与α平行,故错误;
③设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=2a(a>3),则动点P的轨迹是椭圆,故错误;
④若实数k满足0<k<9,则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1的焦点均为(±$\sqrt{34-k}$,0),故正确;
故答案为:①④
点评 本题以命题的真假判断与应用为载体,考查了指数函数的图象和性质,直线与平面位置关系,圆锥曲线的定义和性质,难度中档.

练习册系列答案
相关题目
17.设集合A={n|n=3k-1,k∈Z},B={x||x-1|>3},则A∩(CRB)=( )
| A. | {-1,2} | B. | {-2,-1,1,2,4} | C. | {1,4} | D. | ∅ |
4.已知直线x+my+6=0和(m-2)x+3y+2m=0互相平行,则实数m的取值为( )
| A. | -1或3 | B. | -1 | C. | -3 | D. | 1或-3 |
14.若集合M={x|1<x<4},N={x|x2-7x<0},则M∩N等于( )
| A. | {x|0<x<4} | B. | {x|1<x<7} | C. | {x|1<x<4} | D. | {x|4<x<7} |
1.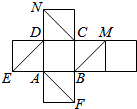 如图是正方体的平面展开图,则在这个正方体中
如图是正方体的平面展开图,则在这个正方体中
①BM与ED成 45°角
②NF与BM是异面直线
③CN与BM成60°角
④DM与BN是异面直线
以上四个结论中,正确结论的个数是( )
 如图是正方体的平面展开图,则在这个正方体中
如图是正方体的平面展开图,则在这个正方体中①BM与ED成 45°角
②NF与BM是异面直线
③CN与BM成60°角
④DM与BN是异面直线
以上四个结论中,正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.方程sinx-$\frac{x}{2014}$=0的零点的个数为( )
| A. | 1280 | B. | 1279 | C. | 1284 | D. | 1283 |
 如图,A,B,C,D都在同一个与水平垂直的平面内,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°.
如图,A,B,C,D都在同一个与水平垂直的平面内,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°.