题目内容

3．在等差数列{an}中，S10=120，那么a1+a10的值是（　　）
A．12B．24C．36D．48

分析 根据等差数列的求和公式，即可求出a1+a10的值．

解答 解：S10=$\frac{1}{2}$×10（a1+a10）=120，
所以a1+a10=24
故选B

点评 本题考查了等差数列的求和公式，属于基础题．

练习册系列答案
相关题目
9．若函数f（x）=x2+bx+c的图象的对称轴为x=2，则函数f（x）的导函数f'（x）的图象不经过（　　）
A．第一象限B．第二象限C．第三象限D．第三象限
10．已知复数z=i（1+2i），则复数z的虚部为（　　）
A．2B．3C．-1D．1
7．函数f（x）的导函数f′（x）的图象如图所示，则（　　）
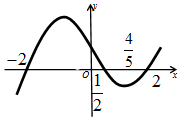
A．$\frac{1}{2}$为f（x）的极大值点B．-2为f（x）的极大值点
C．2为f（x）的极大值D．$\frac{4}{5}$为f（x）的极小值点
14．某家公司每月生产两种布料A和B，所有原料是三种不同颜色的羊毛．下表给出了生产每匹每种布料所需的羊毛量，以及可供使用的每种颜色的羊毛的总量．
羊毛颜色每匹需要/kg供应量/kg
布料A布料B
红331050
绿421200
黄261800
已知生产每匹布料A、B的利润分别为60元、40元．分别用x、y表示每月生产布料A、B的匹数．
（Ⅰ）用x、y列出满足生产条件的数学关系式，并画出相应的平面区域；
（Ⅱ）如何安排生产才能使得利润最大？并求出最大的利润．
8．曲线$\sqrt{1-{{（x-1）}^2}}$=|y-1|-2与直线y=k（x-4）+1有两个不同交点，则实数k的取值范围是[1，$\frac{3-\sqrt{3}}{4}$）∪（$\frac{\sqrt{3}-3}{4}$，-1]． 
15．在?ABCD中，E是CD上一点，且$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{BC}$，AB=2BC=4，∠BAD=60°，则$\overrightarrow{AC}$•$\overrightarrow{EB}$等于（　　）
A．$\frac{1}{2}$B．$\frac{3}{2}$C．2D．3
12．在三棱锥E一ABC中，AB⊥AC，AB=1，AC=$\frac{\sqrt{2}}{2}$，点D在线段BC上，且BD=2CD，ED⊥平面ABC．
（I）证明：AD⊥BE；
（Ⅱ）若AD=DE，求直线CE与平面ABE所成角的正弦值．
13．设点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的右支上，双曲线的左、右焦点分别为F1，F2，若|PF1|=4|PF2|，则双曲线离心率的取值范围是（　　）
A．$（{1，\frac{5}{3}}]$B．（1，2]C．$[{\frac{5}{3}，+∞}）$D．[2，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网