题目内容
12.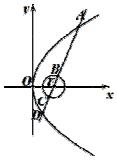 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.
分析 求出|AB|=xA+$\frac{1}{2}$,|CD|=xD+$\frac{1}{2}$,分类讨论,利用基本不等式,求出4|AB|+9|CD|的最小值.
解答 解:∵y2=4x,焦点F(1,0),准线 l0:x=-1
由定义得:|AF|=xA+1,
又∵|AF|=|AB|+$\frac{1}{2}$,∴|AB|=xA+$\frac{1}{2}$
同理:|CD|=xD+$\frac{1}{2}$,
当l⊥x轴时,则xD=xA=1,∴4|AB|+9|CD|=$\frac{39}{2}$;
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,xA+xD=1,
∴4|AB|+9|CD|=$\frac{13}{2}$+4xA+9xD≥$\frac{37}{2}$
综上所述4|AB|+9|CD|的最小值为$\frac{37}{2}$.
故答案为:$\frac{37}{2}$.
点评 本题考查圆与抛物线的综合,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
3.已知函数f(x)=x+sinx(x∈R),当$θ∈({\frac{π}{4},\frac{π}{2}})$时,f(asinθ)+f(1-a)>0恒成立,则实数a的取值范围是( )
| A. | $({0,\frac{{2-\sqrt{2}}}{2}})$ | B. | $({2-\sqrt{2},1})$ | C. | $({1,2+\sqrt{2}}]$ | D. | $({-∞,2+\sqrt{2}}]$ |
20.下列四组函数中,表示同一个函数的是( )
| A. | f(x)=|x+1|,g(x)=$\left\{\begin{array}{l}{x+1(x≥-1)}\\{-1-x(x<-1)}\end{array}\right.$ | B. | f(x)=$\frac{{x}^{2}-1}{x+1}$,g(x)=x-1 | ||
| C. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | D. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ |
17.若点(1,-3)在圆(x-2)2+(y+1)2=m的内部,则实数m的取值范围是( )
| A. | 0<m<10 | B. | 0<m<5 | C. | m>5 | D. | m<5 |
1.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤3}\\{x-y≥-1}\\{y≥1}\end{array}\right.$,则目标函数z=4x+2y的最大值为( )
| A. | 12 | B. | 10 | C. | 8 | D. | 2 |
2.$\frac{{tan{{18}°}+tan{{42}°}+tan{{120}°}}}{{tan{{198}°}tan{{222}°}}}$=( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |