题目内容
2.$\frac{{tan{{18}°}+tan{{42}°}+tan{{120}°}}}{{tan{{198}°}tan{{222}°}}}$=( )| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
分析 利用正切的两角和与差以及诱导公式化简即可.
解答 解:$\frac{{tan{{18}°}+tan{{42}°}+tan{{120}°}}}{{tan{{198}°}tan{{222}°}}}$=$\frac{tan18°+tan42°+tan(180°-60°)}{tan(180°+18°)•tan(180°+42°)}$=$\frac{tan(18°+42°)(1-tan18°tan42°)-tan60°}{tan18°•tan42°}$=-tan60°=-$\sqrt{3}$.
故选A.
点评 本题考查了正切的两角和与差以及诱导公式化简的运用.比较基础.

练习册系列答案
相关题目
10.已知x,y都是正数,且xy=x+y,则4x+y的最小值为( )
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
14.已知f'(x)为定义在$({0,\frac{π}{2}})$上的函数f(x)的导函数,且cosx•f(x)<f'(x)•sinx在$({0,\frac{π}{2}})$上恒成立,则( )
| A. | $\sqrt{3}f({\frac{π}{4}})>\sqrt{2}f({\frac{π}{3}})$ | B. | $\sqrt{2}f({\frac{π}{6}})>f({\frac{π}{4}})$ | C. | $\sqrt{3}f({\frac{π}{6}})<f({\frac{π}{3}})$ | D. | $f(1)<2f({\frac{π}{6}})sin1$ |
11.若关于x的函数f(x)=$\frac{a{x}^{2}+2x+{a}^{2}+sinx}{{x}^{2}+a}$,(a>0)的最大值为M,最小值为N,且M+N=8,则实数a的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.定义区域[x1,x2]的长度为x2-x1(x2>x1),函数$f(x)=\frac{{({a^2}+a)x-1}}{{{a^2}x}}(a∈R,a≠0)$的定义域与值域都是[m,n](n>m),则区间[m,n]取最大长度时实数a的值为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | -3 | C. | 1 | D. | 3 |
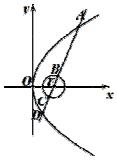 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.