题目内容
4.复数$\frac{2}{i}$=-2i.分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:复数$\frac{2}{i}$=$\frac{-2i}{-i•i}$=-2i,
故答案为:-2i.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.某班主任对全班50名学生进行了作业量多少的调查,根据列联表数据计算得到K2=5.059,因为P(K2≥5.024)=0.025,则认为“喜欢玩电脑游戏与认为作业量的多少有关系”的把握大约为( )
| A. | 2.5% | B. | 95% | C. | 97.5% | D. | 不具有相关性 |
16.已知函数f(x)=sin(2x+$\frac{π}{3}$),则函数f(x)图象的对称轴为( )
| A. | x=$\frac{π}{12}$+kπ(k∈z) | B. | x=$\frac{π}{12}$+$\frac{kπ}{2}$(k∈z) | C. | x=-$\frac{π}{6}$+kπ(k∈z) | D. | x=-$\frac{π}{6}$+$\frac{kπ}{2}$(k∈z) |
14.已知f'(x)为定义在$({0,\frac{π}{2}})$上的函数f(x)的导函数,且cosx•f(x)<f'(x)•sinx在$({0,\frac{π}{2}})$上恒成立,则( )
| A. | $\sqrt{3}f({\frac{π}{4}})>\sqrt{2}f({\frac{π}{3}})$ | B. | $\sqrt{2}f({\frac{π}{6}})>f({\frac{π}{4}})$ | C. | $\sqrt{3}f({\frac{π}{6}})<f({\frac{π}{3}})$ | D. | $f(1)<2f({\frac{π}{6}})sin1$ |
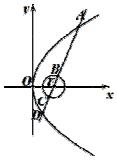 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.