题目内容
2.已知圆x2+y2-2x-4y+3=0关于直线ax+by-1=0(a>0,b>0)对称,则$\frac{1}{a}$+$\frac{2}{b}$的最小值为,9.分析 圆x2+y2-2x-4y+3=0关于直线ax+by-1=0(a>0,b>0)对称,说明直线经过圆心,推出a+2b=1,代入$\frac{1}{a}$+$\frac{2}{b}$,利用基本不等式,确定最小值.
解答 解:由题设直线ax+by-1=0(a>0,b>0)过圆心C(1,2),即a+2b=1,
∴$\frac{1}{a}$+$\frac{2}{b}$=($\frac{1}{a}$+$\frac{2}{b}$)(a+2b)=5+$\frac{2b}{a}$+$\frac{2a}{b}$≥5+4=9,当且仅当a=b时$\frac{1}{a}$+$\frac{2}{b}$的最小值为9,
故答案为:9.
点评 本题考查关于点、直线对称的圆的方程,基本不等式,考查计算能力,是基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
12.点P所在轨迹的极坐标方程为ρ=2cosθ,点Q所在轨迹的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=4+2t}\end{array}\right.$(t为参数),则|PQ|的最小值是( )
| A. | 2 | B. | $\frac{4\sqrt{5}}{5}$+1 | C. | 1 | D. | $\frac{4\sqrt{5}}{5}$-1 |
10.某公司为确定下一年投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年利润y(单位:万元)的影响,对近5年的宣传费xi和年利润yi(i=1,2,3,4,5)进行了统计,列出了下表:
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合y与x的关系,请你建立y关于x的线性回归方程(系数精确到0.01);
(2)小李决定选择对数回归模拟拟合y与x的关系,得到了回归方程:$\widehat{y}$=1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据$\sum_{i=1}^{5}$(yi-$\widehat{y}$i)2=1.15)
参考公式:相关指数R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距的最小二乘法估计公式分别为$\widehat{b}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,参考数据:ln40=3.688,${\sum_{i=1}^5{({x_i}-\overline x)}^2}$=538.
| x(单位:千元) | 2 | 4 | 7 | 17 | 30 |
| y(单位:万元) | 1 | 2 | 3 | 4 | 5 |
(1)小王准备用线性回归模型拟合y与x的关系,请你建立y关于x的线性回归方程(系数精确到0.01);
(2)小李决定选择对数回归模拟拟合y与x的关系,得到了回归方程:$\widehat{y}$=1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据$\sum_{i=1}^{5}$(yi-$\widehat{y}$i)2=1.15)
参考公式:相关指数R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距的最小二乘法估计公式分别为$\widehat{b}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,参考数据:ln40=3.688,${\sum_{i=1}^5{({x_i}-\overline x)}^2}$=538.
17.设数列{an}的通项公式为an=2n-7(n∈N*)则|a1|+|a2|+…+|a7|=( )
| A. | 7 | B. | 0 | C. | 18 | D. | 25 |
11.直线y=2x-2被圆(x-2)2+(y-2)2=25所截得的弦长为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
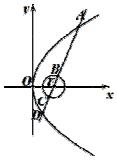 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.