题目内容

19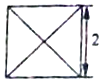．已知某几何体的俯视图是如图所示的边长为2的正方形，主视图与左视图是边长为2的正三角形，则其侧面积（　　）
A．4B．$4\sqrt{3}$C．$4（1+\sqrt{3}）$D．8

分析 由题意可知：原几何体为正四棱锥，侧面斜高为2，底边是2，即可得出．

解答 解：由题意可知：原几何体为正四棱锥，侧面斜高为2，底边是2，可得：侧面积S=4×$\frac{1}{2}×2×2$=8．
故选：D．

点评 本题考查了正四棱锥的三视图及其侧面积计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
9．已知数列{an}满足${a_1}=1，|{{a_n}-{a_{n-1}}}|=\frac{1}{2^n}（{n≥2，n∈N}）$，且{a2n-1}是递减数列，{a2n}是递增数列，则5-6a10=$\frac{1}{512}$．
10．某几何体的三视图如图所示，则该几何体的体积为$\frac{4}{3}$．
7．$\underset{lim}{n→∞}\frac{（2n-3）^{2}}{3{n}^{2}-n+7}$=$\frac{4}{3}$．
14．三棱锥P-ABC中，侧棱PA=2，PB=PC=$\sqrt{6}$，则当三棱锥P-ABC的三个侧面的面积和最大时，经过点P，A，B，C的球的表面积是（　　）
A．4πB．8πC．12πD．16π
4．已知M是函数f（x）=e-2|x-1|+2sin[π（x-$\frac{1}{2}$）]在x∈[-3，5]上的所有零点之和，则M的值为（　　）
A．4B．6C．8D．10
11．设SA为球的直径，B、C、D三点在球面上，且SA⊥面BCD，三角形BCD的面积为3，VS-BCD=3VA-BCD=3，则球的表面积为（　　）
A．16πB．64πC．$\frac{32}{3}$πD．32π
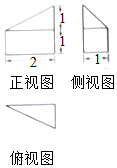
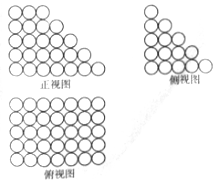8．北宋数学家沈括的主要数学成就之一为隙积术，所谓隙积，即“积之有隙”者，如累棋、层坛之类，这种长方台形状的物体垛积，设隙积共n层，上底由a×b个物体组成，以下各层的长、宽依次各增加一个物体，最下层（即下底）由c×d个物体组成，沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}$[（2b+d）a+（b+2d）c]+$\frac{n}{6}$（c-a）．已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示，则该垛积中所有小球的个数为（　　）
A．83B．84C．85D．86
9．已知集合A={x||x-1|≤2}，B={x|x=2n-1，n∈Z}，则A∩B=（　　）
A．{1，3}B．{0，2}C．{1}D．{-1，1，3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网