题目内容
已知函数f（x）=sin2x向左平移
个单位后，得到函数y=g（x），下列关于y=g（x）的说法正确的是（ ）
| π |
| 6 |
A、一个対称中心为(-
| ||||
B、x=-
| ||||
C、减区间为[
| ||||
D、增区间为[kπ，
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：常规题型,三角函数的图像与性质
分析：先根据图象平移得到函数g（x）的图象，然后结合正弦函数的性质研究g（x）的对称性与单调性．
解答：
解：函数f（x）=sin2x向左平移
个单位后，得到函数f(x)=sin2(x+
)，即f(x)=sin(2x+
)，
令x=-
，得f(-
)=-sin
≠0，A不正确；
令x=-
，得f(-
)=sin0=0≠±1，B不正确；
由-
+2kπ≤2x+
≤
+2kπ，k∈Z，得-
+kπ≤x≤
+kπ，k∈Z，
即函数的增区间为[-
+kπ，
+kπ]，k∈Z，减区间为[
+kπ，
+kπ]，k∈Z，
故选C．
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
令x=-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
令x=-
| π |
| 6 |
| π |
| 6 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
即函数的增区间为[-
| 5π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
故选C．
点评：本题的易错点是函数f（x）=sin2x向左平移
个单位后，得到函数f(x)=sin2(x+
)，即f(x)=sin(2x+
)的图象，而不是得到函数y=sin（2x+
）的图象．
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
练习册系列答案
优加精卷系列答案
相关题目
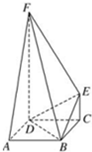如图，FD垂直于矩形ABCD所在平面，CE∥DF，∠DEF=90°．（1）求证：BE∥平面ADF；
（2）若矩形ABCD的一边AB=
| 3 |
| 3 |
| 3 |
十一黄金周期间，5位同学各自随机从“三峡明珠，山水宜昌”、“千古帝乡，智慧襄阳”、“养生山水，长寿钟祥”三个城市中选择一个旅游，则三个城市都有人选的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
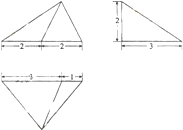若某几何体的三视图（单位：cm）如图所示（依次为正视图、侧视图、俯视图），则此几何体的体积是