题目内容
函数f(x)=
(ax-a-x)(0<a<1),
(1)求证:f(x)为奇函数;
(2)当x∈(-1,1),解不等式f(1-m)+f(m-2)<0;
(3)若f(x)-4当且仅当在x∈(-∞,2)上取负值,求a的值.
| 1 |
| a-a-1 |
(1)求证:f(x)为奇函数;
(2)当x∈(-1,1),解不等式f(1-m)+f(m-2)<0;
(3)若f(x)-4当且仅当在x∈(-∞,2)上取负值,求a的值.
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:(1)利用奇函数的定义,即可得出结论;
(2)结合f(x)的奇偶性与单调性进行求解:由y=f(x)(x∈R)的奇偶性、单调性,由f(1-m)+f(m-2)<0可得f(1-m)<f(2-m),再利用y=f(x)在(-1,1)上是增函数求解m的取值范围.
(3)因为f(x)-4当且仅当在x∈(-∞,2)上取负值,所以f(2)-4=
(a2-a-2)-4=0,整理即可解得a的值.
(2)结合f(x)的奇偶性与单调性进行求解:由y=f(x)(x∈R)的奇偶性、单调性,由f(1-m)+f(m-2)<0可得f(1-m)<f(2-m),再利用y=f(x)在(-1,1)上是增函数求解m的取值范围.
(3)因为f(x)-4当且仅当在x∈(-∞,2)上取负值,所以f(2)-4=
| 1 |
| a-a-1 |
解答:
(1)证明:∵f(-x)=
(a-x-ax)=f(x),x∈R∴f(x)为奇函数;
(2)解:∵0<a<1,∴y=ax-a-x在(-1,1)上是减函数,
∵
<0,
∴y=f(x)在(-1,1)上是增函数.
∵函数f(x)是奇函数,f(1-m)+f(m-2)<0,
∴f(1-m)<f(2-m),
∴1-m<2-m且-1<1-m<1,-1<2-m<1,
∴1<m<2,
故不等式的解集{m|1<m<,2};
(3)因为f(x)-4当且仅当在x∈(-∞,2)上取负值,
所以f(2)-4=
(a2-a-2)-4=0,
整理得a2-4a+1=0,
因为0<a<1,所以a=2-
.
| 1 |
| a-a-1 |
(2)解:∵0<a<1,∴y=ax-a-x在(-1,1)上是减函数,
∵
| 1 |
| a-a-1 |
∴y=f(x)在(-1,1)上是增函数.
∵函数f(x)是奇函数,f(1-m)+f(m-2)<0,
∴f(1-m)<f(2-m),
∴1-m<2-m且-1<1-m<1,-1<2-m<1,
∴1<m<2,
故不等式的解集{m|1<m<,2};
(3)因为f(x)-4当且仅当在x∈(-∞,2)上取负值,
所以f(2)-4=
| 1 |
| a-a-1 |
整理得a2-4a+1=0,
因为0<a<1,所以a=2-
| 3 |
点评:本题是函数奇偶性与单调性的综合应用,特别是后面抽象不等式及恒成立问题,难度较大.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
函数f(x)=-|x-5|+2x-1的零点所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
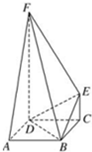 如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.
如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.