题目内容
抛物线y2=2px（p＞0）的焦点为F，准线为l，经过F的直线与抛物线交于A，B两点，交准线于C点，点A在x轴上方，AK⊥l，垂足为K，若|BC|=2|BF|，且|AF|=4，求△AKF的面积．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：分别B作准线的垂线，利用抛物线定义将A、B到焦点的距离转化为到准线的距离，结合已知比例关系，求△AKF的底边长和高，可得答案．
解答：
解：过B作BE垂直于抛物线的准线，垂足为E，P为准线与x轴的焦点，
由抛物线的定义，|BF|=|BE|，|AF|=|AK|=4，
∵|BC|=2|BF|，
∴|BC|=2|BE|，
∴∠KCA=30°，
故|AF|=|AK|=4，
F点到AK的距离d=4×cos30°=2
，
故△AKF的面积S=
×AK×d=4
．
由抛物线的定义，|BF|=|BE|，|AF|=|AK|=4，
∵|BC|=2|BF|，
∴|BC|=2|BE|，
∴∠KCA=30°，
故|AF|=|AK|=4，
F点到AK的距离d=4×cos30°=2
| 3 |
故△AKF的面积S=
| 1 |
| 2 |
| 3 |
点评：本题考查抛物线的定义及其应用，抛物线的几何性质，过焦点的弦的弦长关系，转化化归的思想方法，属中档题．
练习册系列答案
相关题目
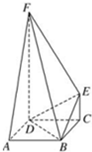如图，FD垂直于矩形ABCD所在平面，CE∥DF，∠DEF=90°．（1）求证：BE∥平面ADF；
（2）若矩形ABCD的一边AB=
| 3 |
| 3 |
| 3 |
已知|lga|=lgb（a＞0，b＞0），那么（ ）
| A、a=b | B、a=b或ab=1 |
| C、a=±b | D、ab=1 |
十一黄金周期间，5位同学各自随机从“三峡明珠，山水宜昌”、“千古帝乡，智慧襄阳”、“养生山水，长寿钟祥”三个城市中选择一个旅游，则三个城市都有人选的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|