题目内容
4.将函数$f(x)=sin({x+\frac{π}{6}})$的图象上各点的纵坐标不变,横坐标扩大到原来的2倍,所得函数g(x)图象的一个对称中心可以是( )| A. | $({-\frac{π}{12},0})$ | B. | $({\frac{5π}{12},0})$ | C. | $({-\frac{π}{3},0})$ | D. | $({\frac{2π}{3},0})$ |
分析 根据y=Asin(ωx+∅)的图象变换规律可得所得图象对应的函数为y=sin($\frac{1}{2}$x+$\frac{π}{6}$),由$\frac{1}{2}$x+$\frac{π}{6}$=kπ,k∈z,可得对称中心的横坐标,从而得出结论.
解答 解:∵$g(x)=sin({\frac{1}{2}x+\frac{π}{6}})$,
∴由$\frac{x}{2}+\frac{π}{6}=kπ$,∴$可得x=2kπ-\frac{π}{3},k∈Z$,
令$k=0,x=-\frac{π}{3}$.
故选:C.
点评 本题主要考查y=Asin(ωx+∅)的图象变换规律,正弦函数的对称中心,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
14.已知2x=7y=k,$\frac{1}{x}$-$\frac{1}{y}$=4,则k的值是( )
| A. | ($\frac{2}{7}$)${\;}^{\frac{1}{4}}$ | B. | ($\frac{2}{7}$)4 | C. | 5${\;}^{\frac{1}{4}}$ | D. | ($\frac{7}{2}$)${\;}^{\frac{1}{4}}$ |
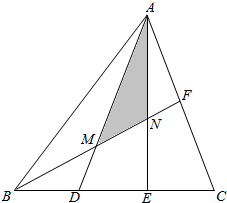 △ABC中,D、E三等分BC,F为AC的中点,BF分别与AD、AE交于M、N.试求△AMN与△ABC面积之比.
△ABC中,D、E三等分BC,F为AC的中点,BF分别与AD、AE交于M、N.试求△AMN与△ABC面积之比.